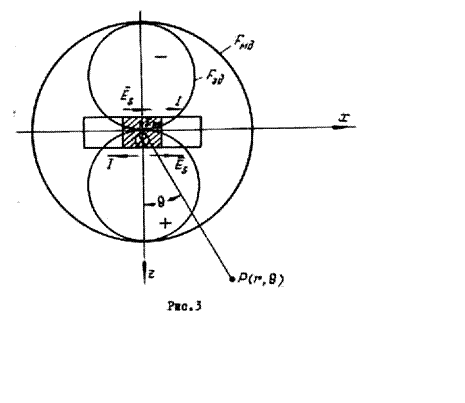
Диаграмма направленности
электрического диполя в этой плоскости имеет форму «восьмерки», а магнитного
диполя - форму окружности. Поскольку электрические токи со стороны ![]() и
и ![]() направлены
в противоположные стороны, то поля, излучаемые ими в полупространста
направлены
в противоположные стороны, то поля, излучаемые ими в полупространста ![]() и
и ![]() будут
находиться в противофазе, и диаграмму направленности с учетом фазы можно записать
в виде
будут
находиться в противофазе, и диаграмму направленности с учетом фазы можно записать
в виде
![]()
где ![]()
Магнитные токи со стороны ![]() и
и ![]() также
протекают в противоположных направлениях, однако создаваемое ими электрическое
поле в соответствии с выражением (2) имеет одинаковое направление вектора
также
протекают в противоположных направлениях, однако создаваемое ими электрическое
поле в соответствии с выражением (2) имеет одинаковое направление вектора ![]() в обоих полупространствах
в обоих полупространствах ![]() и
и ![]() .
Поэтому диаграмму направленности магнитного диполя можно записать в виде
.
Поэтому диаграмму направленности магнитного диполя можно записать в виде
![]()
Поле, создаваемое каждым из
диполей в произвольной точке ![]() плоскости
плоскости ![]() с учетом вида диаграмм (4) и (5), будет
определяться выражениями
с учетом вида диаграмм (4) и (5), будет
определяться выражениями
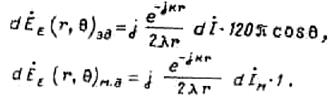
Складывая поля обоих
элементарных источников, получаем поле элементарной площадки в плоскости ![]() :
:
![]()
С учетом выражений (3) и (1) окончательно получаем
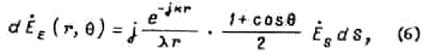
где ![]()
Выражение
![]()
представляет собой нормированную ДН элементарной
площадки в плоскости ![]() . Вид диаграммы показан на рис.4.
. Вид диаграммы показан на рис.4.
Поле в плоскости ![]() . Плоскость
. Плоскость ![]() в нашем
случае совпадает с плоскостью
в нашем
случае совпадает с плоскостью ![]() . На рис.5 в начало
координат помещены электрический и магнитный диполи. Сравнивая этот рисунок с
рис.3, замечаем, что электрический и магнитный диполи поменялись местами
(здесь
. На рис.5 в начало
координат помещены электрический и магнитный диполи. Сравнивая этот рисунок с
рис.3, замечаем, что электрический и магнитный диполи поменялись местами
(здесь
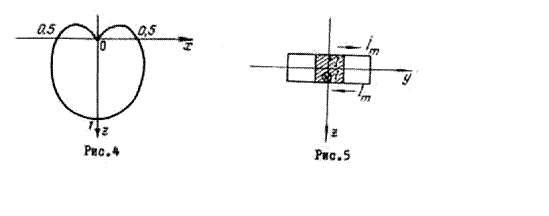
заштрихован электрический диполь).
Это позволяет нам для нахождения
ДН в плоскости ![]() воспользоваться принципом
взаимности.
воспользоваться принципом
взаимности.
В формуле (6) произведем замену:
![]() на
на ![]() ,
, ![]() на
на ![]() ,
, ![]() на
на ![]() и
и ![]() на
на ![]() . В
результате получаем
. В
результате получаем
![]()
Учитывая, что ![]() и
и ![]() , также
имеем
, также
имеем
![]()
Отсюда следует, что так же, как и в плоскости ![]() , ДН элементарной площадки в плоскости
, ДН элементарной площадки в плоскости ![]() описывается выражением
описывается выражением
![]()
Итак, ДН элементарной площадки одинакова в обеих главных
плоскостях ![]() и
и ![]() и имеет
вид
и имеет
вид
![]()
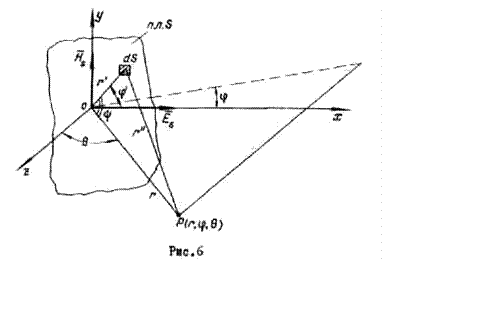
Предположим, что имеется
некоторая площадка ![]() произвольной формы, лежащая в
плоскости
произвольной формы, лежащая в
плоскости ![]() (рис.6). Пусть на ней существует
электромагнитное поле с произвольным распределением:
(рис.6). Пусть на ней существует
электромагнитное поле с произвольным распределением:
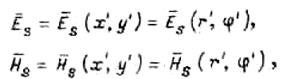
векторы ![]() и
и ![]() лежат в плоскости площадки (вектор
лежат в плоскости площадки (вектор ![]() параллелен оси
параллелен оси ![]() , вектор
, вектор
![]() параллелен оси
параллелен оси ![]() ) и
связаны соотношением
) и
связаны соотношением ![]() . Определим поле такой площадки в
дальней зоне.
. Определим поле такой площадки в
дальней зоне.
Поле, создаваемое элементарной
площадкой ![]() в некоторой точке наблюдения
в некоторой точке наблюдения ![]() , можно записать в виде
, можно записать в виде
![]()
Тогда поле площадки конечных размеров определяется соотношением
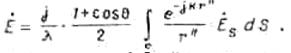
Для дальней зоны ![]() . Поэтому с точки зрения амплитуды можно
положить
. Поэтому с точки зрения амплитуды можно
положить ![]() , а в экспоненте заменить
, а в экспоненте заменить ![]() величиной
величиной ![]() . Тогда
. Тогда
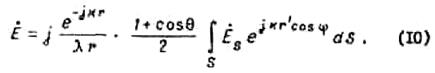
Величину ![]() в этой формуле можно
выразить соотношениями:
в этой формуле можно
выразить соотношениями:
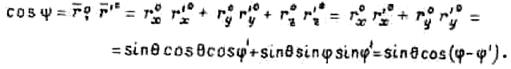
Здесь ![]() и
и ![]() - орты в направлении
- орты в направлении ![]() и
и ![]() .
.
 Вычисление
поля в общем случае весьма громоздко. Аналитическое решение получается лишь
для ряда частных случаев. Часто задачу сужают и рассматривают поле лишь в
главных плоскостях
Вычисление
поля в общем случае весьма громоздко. Аналитическое решение получается лишь
для ряда частных случаев. Часто задачу сужают и рассматривают поле лишь в
главных плоскостях ![]() и
и ![]() .
.
Рассмотрим некоторые из этих случаев.
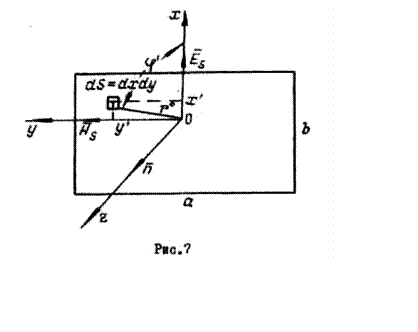
Поле прямоугольной площадки. 1. Прежде всего рассмотрим прямоугольную площадку (рис.7) с равномерным распределением поля:
![]()
Поле в плоскости ![]() (
(![]() ). В этой
плоскости
). В этой
плоскости ![]() ,
, 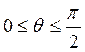 и
общая формула для поля приобретает
и
общая формула для поля приобретает
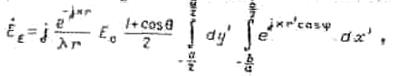
где
![]()
Проинтегрировав по ![]() и
и ![]() , получим
, получим
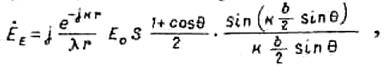
где ![]() - площадь площадки.
- площадь площадки.
Поле в плоскости ![]() . В этой
плоскости
. В этой
плоскости ![]() ,
, ![]() ,
следовательно,
,
следовательно,
![]()
и выражение для поля после преобразований имеет вид
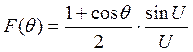
Анализируя полученные
соотношения, замечаем, что в обеих плоскостях (![]() и
и ![]() ) поле описывается одинаковыми функциями,
функция, характеризующая диаграмму направленности, имеет вид
) поле описывается одинаковыми функциями,
функция, характеризующая диаграмму направленности, имеет вид
![]()
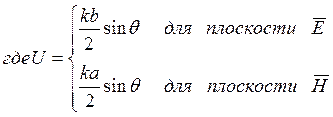
при "косинусоидальном" распределении поля
шире, чем в плоскости ![]() , но зато существенно ниже
уровень боковых лепестков.
, но зато существенно ниже
уровень боковых лепестков.
Зная значения ![]() на
уровне половинной мощности (0,707 по напряженности поля), можно вычислить
ширину диаграммы направленности.
на
уровне половинной мощности (0,707 по напряженности поля), можно вычислить
ширину диаграммы направленности.
Функция ![]() в
0,707 при
в
0,707 при 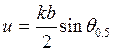 = 1,394, и ширина диаграммы в
плоскости
= 1,394, и ширина диаграммы в
плоскости ![]() определяется выражение
определяется выражение 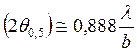 или
или 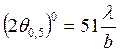
Функция 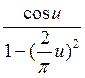 = 0,707
при
= 0,707
при 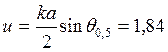 ,поэтому диаграмма направленности в
плоскости
,поэтому диаграмма направленности в
плоскости ![]() имеет ширину
имеет ширину 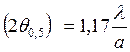 или
или
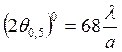
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.