Основные электрические параметры антенн. Эффективная площадь антенны А, страница 30

Введя обозначения O^`M=R_y OM=у' и используя правило приближенного вычисления корня для случая, когда у'«R_y

получим, что

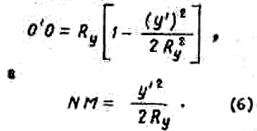
Подставив выражение (6) в (5), получим

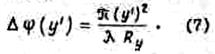
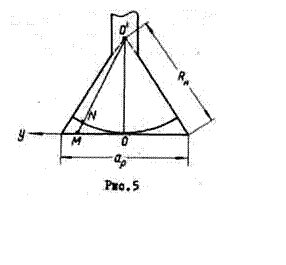
Максимальный сдвиг по фазе имеет место на краю рупора. Он определяется формулой

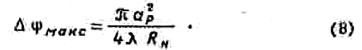
Коэффициент направленного действия  Н - плоскостного секториалъного рупора зависит от площади раскрыва а_р b_p и коэффициента ее использования , т.е.

Коэффициент  зависит от амплитудно-фазового распределения поля на раскрыве и падает по мере роста

Как видно из выражения (8),  связан с размером раскрыва а_р квадратичной зависимостью. Поэтому при неизменной длине рупора R_н в случае малых а_р вначале происходит  рост к.н.д. (за счет увеличения а_р ), при некотором значении а_р D_H достигает своего максимального значения, а дальнейшее увеличение а_р  вызывает уменьшение D_H. Замедление роста D_H, а затем и его уменьшение вызвано возрастание* фазового сдвига по мере роста а_р (это вызывает снижение коэффициента использования площади раскрыва  ).

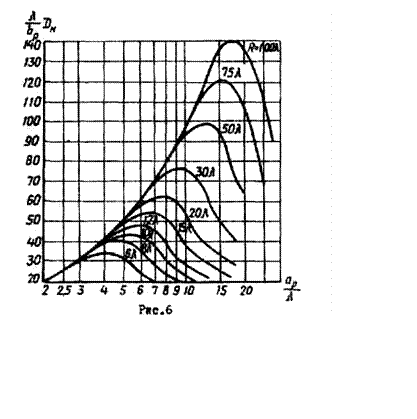
На рис.6 построен ряд кривых, характеризующих зависимость D_H

от отношения  для рупоров разной длины R_H . Каждому значению длины рупора R_H соответствует определенная величина , при которой коэффициент направленного действия  D_H  достигает максимального значения. Рупор, который при заданной длине обладает максимальным к.н.д. D_H, называется оптимальным. Установлено, что оптимальному рупору соответствует вполне определенный фазовый сдвиг . Для рупоров с расширением в плоскости Н

Используя последнее равенство и выражение (8), можно получить формулу, связывающую длину оптимального рупора  R_{н onm},  размер раскрыва а_р  и длину волны в виде

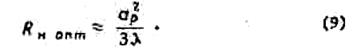
Ширину диаграммы направленности на уровне половинной мощности можно выразить соотношением

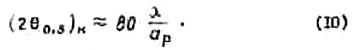
СЕКТОРИАЛЬНЫЙ РУПОР С РАСШИРЕНИИ В ПЛОСКОСТИ   Е

Поле в раскрыве такого рупора (рие.7) можно приближенно представить выражением

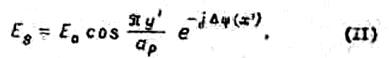
Оно мало отличается от поля в волноводе. В отличие от рассмотренного ранее  Н -плоскостного рупора фазовая скорость в

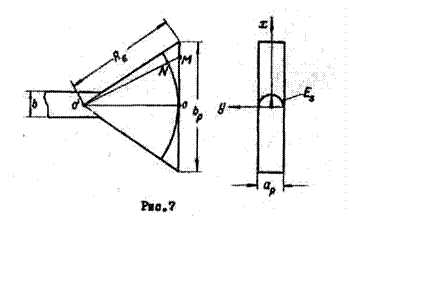
Е -плоскостном рупоре оказывается такой же, как и в волноводе, т,в.

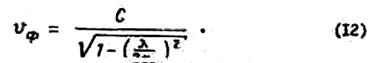
Поле в Е -плоскостном секторальном рупоре отличается of поля в волноводе цилиндрической формой фронта волны. Вследствие этого в раскрыве рупора имеют место фазовые искажения» аналогичные фазовым искажениям в Н- плоскостном секторальном рупоре. Проводя рассуждения, подобные тем, которые имели место при рассмотрении Н-плоскостного рупора, можно показать, что фазовый сдвиг

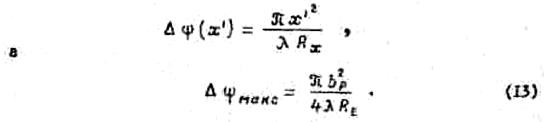
Кривые зависимости D_Е от отношения  для рупоров разной длины q показаны на рис,8. Ход кривых качественно соответствует ходу кривых для

Н -плоскостных рупоров (рис.6). Однако так как в плоскости Е имеет место равномерное распределение поля, то фазовый сдвиг на краю раскрыва Е-плоскостного рупора оказывает большее влияние на коэффициент направленного действия антенны. По этой причине оптимальному Е-плоскостному рупору соответствует меньшее значение

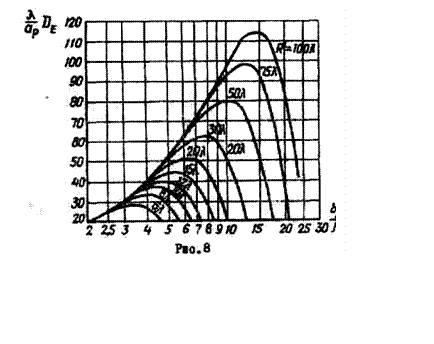
Найдено, что максимумы кривых на рис.8 соответствуют фазовому сдвигу                                                 

После подстановки этого значения формулу (13) и несложных преобразований получим, что

ПИРАМИДАЛЬНЫЕ РУПОРЫ

Фронт волны в пирамидальном рупоре приближенно принимают за сферический. Фазовые искажения в раскраве пирамидального рупора определяются выражением

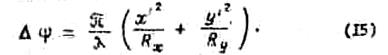
Структура поля в плоскостях Е и Н совпадает со структурой поля в этих же плоскостях в Е - и Н -плоскостных секторальных рупорах соответственно. Вследствие этого при расчетах, пирамидальных рупоров можно пользоваться графиками рис.б и 8.

С.А.Щепкуновым показано, что коэффициент направленного действия любого пирамидального рупора

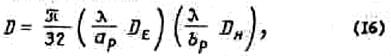
где     D_E - коэффициент направленного действия E-плоскостного   секторального рупора, размер которого равен соответствующему размеру пирамидального рупора;

D_н - коэффициент направленного действия Н -плоскостной секторального рупора, размер которого равен соответствующему размеру пирамидального рупора.