Основные электрические параметры антенн. Эффективная площадь антенны А, страница 28

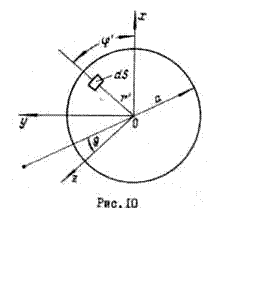
Поле круглой площадки. Рассмотрим случай, когда поле на круглой площадке меняется только по радиусу. Для определения поля произведем некоторые преобразования в основной расчетной формуле, описывающей поле площадки произвольной формы. Элемент  (рис.10) в данном случае удобно выразить в полярной системе координат :

и интегрирование произвести по координатам г' и  ' . В результате получим

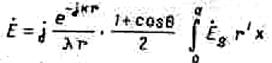
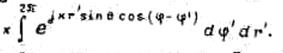
После введения нормированной координаты 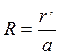и обозначения

ц- каsin6 формула преобразуется к виду

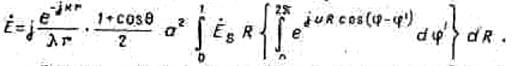
Интеграл в фигурных скобках равен величине , где функция Бесселя нулевого порядка.

Таким образом, окончательно получим

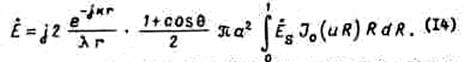
Рассмотрим случай, когда поле меняется по радиусу следующим образом:

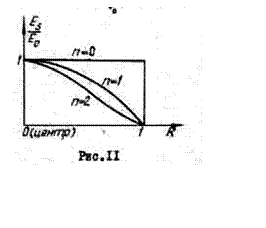
Эта формула охватывает случаи, когда попе вообще не изменяется (n-о) или плавно убывает до нуля от центра к краю площадки. Удобно пользоваться нормированным распределением

Графики этого распределения для различных n показаны на  рис.II.

Для определения, поля круглой площадки подставим в формулу (14) значение  из выражения (15). Интеграл

сводится к 1-функции (n+1 )-го порядка и равен

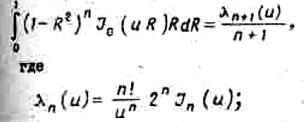
Jn(U)- функция Бесселя n -то порядка.

Следовательно, окончательно поле можно охарактеризовать формулой

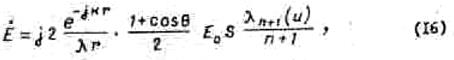
а ДН записать в виде выражения

Если размеры площадки велики по сравнению с длиной волны, то изменением первого множителя 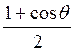 можно пренебречь, поскольку

- функция меняется намного быстрее. В результате этого для случаев, когда a >>,

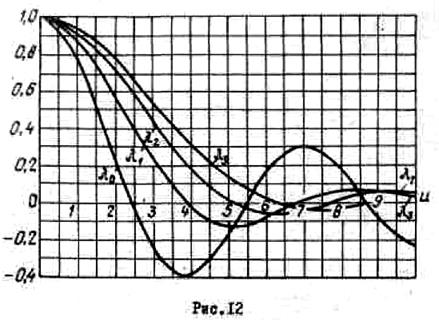
На рис.12 изображены графики  - функций.

Пусть, например, поле равномерно: n=0, 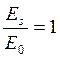. Тогда в соответствии с формулой (18) F(0)=(u). Ширина диаграммы на уровне половинной мощности может быть найдена из условия

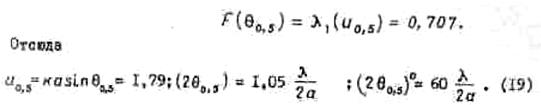
В заключение сделаем некоторые общие выводы.

1. При синфазном возбуждении площадки произвольной формы максимум излучения перпендикулярен плоскости площадки.

2. Убывание амплитуды поля от середины площадки к ее краям вызывает некоторое расширение главного лепестка, но при этом снижается уровень боковых лепестков.

3. С увеличением размеров площадки диаграмма направленности становится уже.

КОЭФФИЦИЕНТ НАПРАВЛЕННОГО ДЕЙСТВИЯ И ЭФФЕКТИВНАЯ ПОВЕРХНОСТЬ ПЛОЩАДОК

Коэффициент направленного действия антенн СВЧ удобно определять через их эффективную поверхность А :

Эффективная поверхность определяется выражением

Для площадок, возбуждаемых синфазным полем,

Рассмотрим, каково соотношение между эффективной поверхностью А и геометрической площадью S площадок при некоторых законах распределения поля.

I. Площадка произвольной формы, возбуждаемая равномерно:

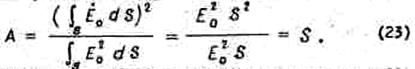
Таким образом, при синфазном и равноамплитудном поле эффективная поверхность площадки равна ее геометрической площади.

2. Прямоугольная площадка с косинусоидальным изменением амплитуды синфазного поля:

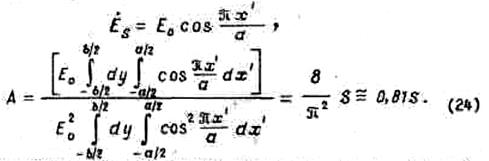
В данном случае эффективная поверхность составляет около 81% геометрической. То, что при неравноамплитудном возбуждении площадки ее эффективная поверхность оказывается меньше геометрической, является естественным. Действительно, в рассматриваемом случае амплитуда поля к краям площадки убывает и, следовательно, элементы площадки, более близкие к краям, будут создавать меньшую напряженность поля, чем элементы площадки, расположенные в середине. Ослабление поля к краям площадки эквивалентно уменьшению ее размеров, если ее рассматривать как возбуждаемую равномерно.

Тема 9

РУПОРНЫЕ АНТЕННЫ

Открытый конец волновода является источником интенсивного излучения (размеры поперечного сечения волновода соизмеримы с длиной волны), т.е. он представляет собой весьма эффективную антенну. Но такие антенны дают, как правило, слабонаправленное излучение и сравнительно плохо согласованы с окружающим пространством.

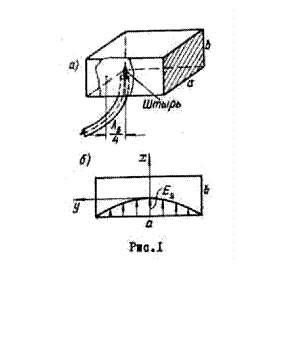
На рис. 1,а показан вариант реализации антенны в виде открытого конца прямоугольного волновода, возбуждаемого волной типа Н₁₀ .