Так, если ![]() = 0,8, то дифракционные максимумы появляются при
= 0,8, то дифракционные максимумы появляются при ![]() как в решетке слабонаправленных излучателей,
так и в решетке рупоров (рис.3 и 4). Но в первом случае при дальнейшем
увеличении
как в решетке слабонаправленных излучателей,
так и в решетке рупоров (рис.3 и 4). Но в первом случае при дальнейшем
увеличении ![]() дифракционный максимум быстро растет,
достигая значения 0,42 при
дифракционный максимум быстро растет,
достигая значения 0,42 при ![]() (рис.3),
(рис.3),
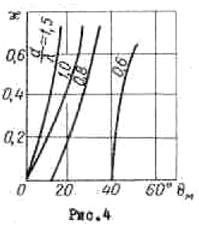 а во втором - дифракционный максимум растет
значительно медленнее, достигая при
а во втором - дифракционный максимум растет
значительно медленнее, достигая при ![]() величины
0,18 ( рис.4 ).
величины
0,18 ( рис.4 ).
Наилучшей ДН излучателя решетки была бы диаграмма, соответствующая по форме прямоугольнику (в декартовых координатах). Если при этом ширина прямоугольника соответствовала бы сектору движения луча, то отклонение ДН от нормали к решетке не вызывало бы расширения главного лепестка и дифракционные лепестки были бы подавлены. Но создание диаграмм направленности такой формы наталкивается на ряд трудностей. Необходимо увеличивать размеры раскрыва и создавать на нем специальное амплитудно-фазовое распределение поля.
Целесообразно также в качестве излучателей решетки использовать диэлектрические, спиральные или директорные антенны, отличительной особенностью которых является то, что они при сравнительно малых поперечных размерах обладают большей направленностью, чем другие известные типы антенн.
Выбор числа излучателей решетки. При проектировании антенных решеток с управляемой диаграммой направленности следует стремиться к наименьшему числу излучателей, так как только в этом случае система получится наиболее простой, надежной и дешевой.
Минимальное число излучателей ![]() , при котором может быть реализована
антенная решетка с заданными параметрами, определяется формулой
, при котором может быть реализована
антенная решетка с заданными параметрами, определяется формулой
![]()
где ![]() - заданный сектор
движения луча;
- заданный сектор
движения луча;
![]() - требуемая ширина
диаграммы направленности решетки на уровне половинной мощности.
- требуемая ширина
диаграммы направленности решетки на уровне половинной мощности.
Выражение (21) справедливо для решетки излучателей с равно-амплитудными токами при линейном законе изменения фазы.
ДВУМЕРНЫЕ АНТЕННЫЕ РЕШЕТКИ
Для формирования антенного луча в двух взаимно перпендикулярных плоскостях и обеспечения возможности управления его положением в некотором пространственном секторе необходимо использовать двумерную (плоскую) решетку излучателей.
На практике находят применение плоские, цилиндрические, сферические, конические и другие типы антенных решеток. В ряде случаев тип решетки определяется формой элемента конструкции объекта, на котором размещается антенная система (крыло, фюзеляж или хвостовое оперение самолета, носовая или хвостовая часть ракеты, часть поверхности космического аппарата и т.п.). Анализ поля излучения криволинейных решеток (особенно неправильной формы) в общем случае весьма сложен. Однако если решетка является остронаправленной, то для расчета ее поля излучения можно, воспользовавшись методом эквивалентного плоского раскрыва, вместо криволинейной рассмотреть некоторую эквивалентную ей плоскую решетку.
Таким образом, приводимый ниже анализ направленных свойств плоской решетки может быть распространен также и на более сложные двумерные решетки.
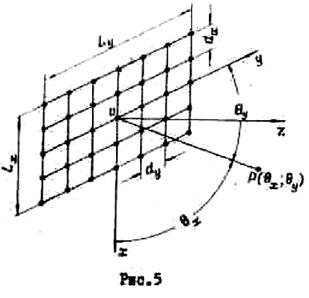
На рис.5 изображена плоская решетка идентичных и одинаково ориентированных излучателей. Если, кроме того, токи всех излучателей равны по амплитуде, фазы токов вдоль осей ox и оу меняются по линейным законам, а расстояние между соседними излучателями равны dx вдоль оси оx и dy вдоль оси оу, то для расчета ДН решетки можно применить теорему перемножения.
Согласно этой теореме ДН линейной решетки
![]()
где ![]() - пространственная
диаграмма направленности излучателя решетки;
- пространственная
диаграмма направленности излучателя решетки;
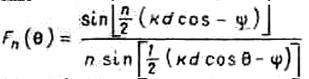
- множитель решетки (здесь ![]() , если
решетка ориентирована вдоль оси ox и
, если
решетка ориентирована вдоль оси ox и![]() , если решетка
ориентирована вдоль оси оу ).
, если решетка
ориентирована вдоль оси оу ).
При решении нашей задачи представим рассматриваемую плоскую решетку (5), как линейную, ориентированную вдоль оси ох, каждый излучатель которой, в свою очередь, также представляет собой линейную решетку, но ориентированную параллельно оси оу .
Применение соотношения (22) к линейной решетке, ориентированной вдоль оси оу, дает
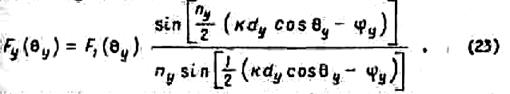
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.