Основные электрические параметры антенн. Эффективная площадь антенны А, страница 26

                    (11)

а при продольных

                           (12)

В плоскости  ДН обостряется. При достаточно большом числе щелей и равноамплитудном возбуждении ДН может быть представлена приближенным выражением

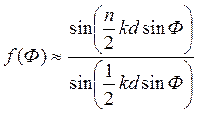                 (13)

Примерный вид ДН синфазных волноводно-щелевых антенн в пл.  изображен на рис.9,б.

В волноводно-щелевых антеннах бегущей волны на конце волновода, питающего щели, устанавливается поглощающая нагрузка (рис.10). ДН такой антенны, пользуясь теоремой перемножения, можно представить выражением

где

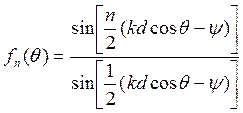
Сдвиг по фазе  между токами в соседних щелях зависит от расстояния между ними   и длины волны в волноводе , где .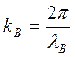

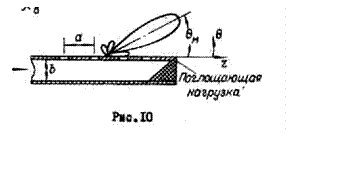
Положение главного максимума диаграммы направленности   (рис.10)  может  быть  найдено  при  помощи  формулы

Откуда

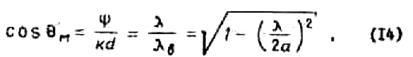
Если используются продольные щели, прорезанные, как показано на рис.8, или продольные щели со штырями (рис.9), то  при нахождении  нужно учитывать дополнительный скачок фазы на . С его учетом

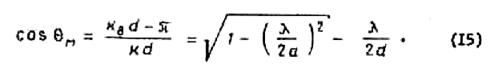
Волноводно-щелевые  антенны  бегущей  волны  находят применение  для осуществления  электрического  или   электромеханического качания луча. Эту задачу можно решить изменением частоты питающего генератора или изменением параметров волновода: в частности, можно менять размер, а путем перемещения одной из узких стенок. При этом будут изменяться сдвиг по фазе  и положение луча в пространстве.

Тема 8

ОСНОВЫ ТЕОРИИ АНТЕНН СВЧ

Для излучения электромагнитных волн СВЧ диапазона широкое применение находят так называемые поверхностные антенны. В общем  случае поверхностную антенну можно представить как площадку, на которой определенным образом распределено электромагнитное поле. Если на ней выделить бесконечно малый элемент, то получим элементарный источник излучения (элементарную площадку, или источник Гюйгенса).

Поле излучения поверхностной антенны в соответствии с принципом суперпозиции образуется из совокупности полей, излучаемых каждой из элементарных площадок. Поэтому для определения поля излучения поверхностной антенны необходимо прежде всего знать поле, которое создается элементарной площадкой.

ПОЛЕ ИЗЛУЧЕНИЯ ЭЛЕМЕНТАРНОЙ ПЛОЩАДКИ

Пусть через площадку , лежащую в плоскости , в направлении оси  распространяется плоская волна. Величины  и  в этом случае, как известно, связаны соотношением

Направления векторов  и  совместим с координатными осями  и .

Рассмотрим на этой площадке элемент  центр которого совпадает с началом координат. Вследствие малости размеров элементарной площадки поле в ее пределах можно считать равномерным.

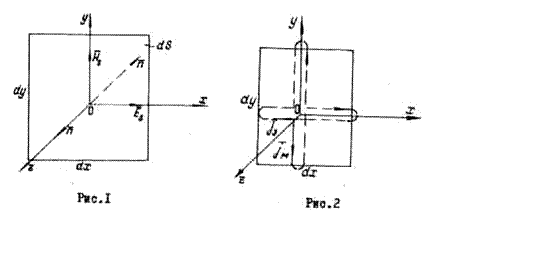
Для определения поля, излучаемого элементарной площадкой, рассмотрим ее обособленно, выделив из площадки  (рис.1). Если ввести электрические и магнитные токи

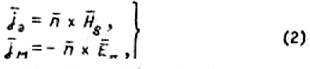
где      - нормаль к плоскости, то электромагнитное поле на площадке можно заменить эквивалентными токами, обтекающими ее (рис.2):                                                                                      

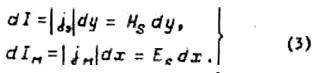
При этом на задней стороне площадки направления токов совпадают с направлением векторов поля, а на передней - противоположно им. Отсюда следует, что элементарная площадка, заполненная

электромагнитным полем, эквивалентна электрическому и магнитному диполям, совмещенным в пределах площадки, оси которых соответственно лежат в плоскостях векторов  и .

Поскольку элементарная площадка эквивалентна сумме элементарных источников, то поле, излучаемое ею, может быть найдено путем сложения полей данных источников. Определение выражения для поля элементарной площадки в общем виде связано с громоздкими математическими выкладками. Поэтому мы найдем только выражения, описывающие поле в главных плоскостях: плоскости, в которой лежит вектор  (плоскости ), и плоскости, в которой расположен вектор .(плоскости ).

Поле  в  плоскости . В нашем случае плоскость  совпадает с плоскостью . Поместим в начало координат (рис.3) электрический и магнитный диполи (магнитный диполь заштрихован). Ось электрического диполя совпадает с осью, a магнитного - с осью , направленной перпендикулярно к плоскости чертежа. В соответствии с рис.2 обозначим направления токов.