Физика \ Антенны и устройство СВЧ

Основные электрические параметры антенн. Эффективная площадь антенны А, страница 49

При нашем представлении вдоль оси ох расположено nx излучателей, ДН каждого из которых  описывается функцией . Поэтому повторное применение теоремы перемножения позволяет записать ДН плоской решетки в виде зависимости

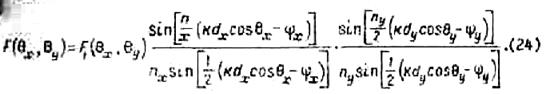
Сами излучатели и расстояния между ними dx и dy, a также сектор качания, луча следует выбирать таким образом, чтобы исключить появление дифракционных максимумов недопустимо большой интенсивности.

Полагая вначале для упрощения рассуждений, что излучатели изотропны, т.е. , проведем исследование выражения

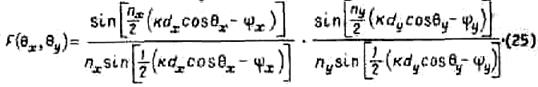
Направление главного максимума антенного луча плоской решетки  можно найти, приравняв единице соотношение (25), т.е.

Последнее, как известно, может иметь место лишь в случаях, когда

Отсюда получаем, что

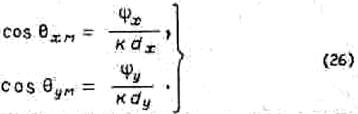
Диаграмма направленности линейной решетки изотропных излучателей представляет собой тело вращения вокруг ее оси (оx или оу). Поэтому прямые, соответствующие направлениям главных максимумов, образуют в пространстве конус, ось которого совпадает с линией расположения излучателей решетки ох или оу, а угол при вершине  или  определяется одним из выражений (26).

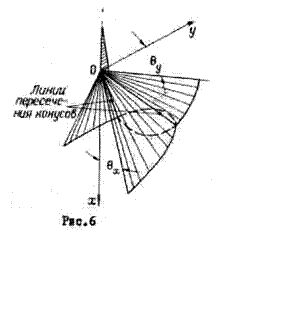
Направления главных максимумов антенного луча плоской решетки определяются пиниями пересечения двух конусов, оси которых ох и оу взаимно перпендикулярны (рис.6). В частном случае, когда конусы касаются друг друга, решетка имеет один главный максимум (в плоскости хоу). Нетрудно показать, что при этом и, следовательно, справедливо равенство  

В общем случае   и конусы имеют две линии пересечения. Это означает, что у плоской решетки будет два главных максимума (в передней и задней полусферах). Однако в реальных решетках благодаря использованию однонаправленных излучателей возможность появления второго максимума исключается.

По мере отклонения луча от направления нормали к решетке происходит его расширение. Используя формулу (7), можно для плоской решетки написать зависимости                                                                                           

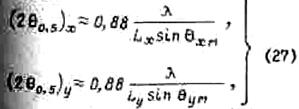
где заменен на   и соответственно, так как отсчет углов здесь производится от плоскости решетки.

Подпись:           При построении решеток с управляемыми диаграммами направленности весьма важным является выбор числа излучателей и управляющих устройств.

Элементарные расчеты показывают, что для формирования острых игольчатых лучей () требуются сотни и тысячи излучателей и соответственно такое же число управляющих устройств. И если еще изготовить сами излучатели не составляет большого труда, то существенные трудности возникают с управляющими устройствами, - наиболее сложными элементами системы. Большое их число приводит к усложнению схемы и удорожанию конструкции. По этой причине следует рассмотреть вопрос о минимальном числе излучателей и управляющих устройств при двумерном движении луча.

Если в плоскости xoz заданы сектор движения луча  и ширина диаграммы направленности , то по аналогии с выражением (21) для линейных решеток можно записать

При движении луча в двух плоскостях систему из nxмин элементов, обеспечивающую качание луча в одной плоскости, следует рассматривать как один элемент новой системы из nyмин излучите лей, для которой справедливо соотношение

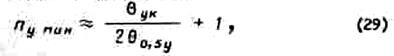
где и - сектор движения и ширина луча в плоскости уоz .

Таким образом, число элементов в решетке с двумерным движением луча определяется выражением

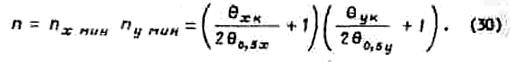
СПОСОБЫ ЭЛЕКТРИЧЕСКОГО УПРАВЛЕНИЯ ДН

В основе электрического управления ДН лежит фазовый принцип. Суть его состоит в том, что изменение положения антенного луча достигается за счет изменения фазового сдвига между токами в излучателях решетки. На практике применяются два способа электрического управления:

I) фазовое управление - управление при помощи изменения фазового сдвига между токами в излучателях;

2)частотное управление-управление при помощи изменения частоты питающего генератора (изменение частоты вызывает изменение фазового сдвига между токами в излучателях).

Скачать файл