Основные электрические параметры антенн. Эффективная площадь антенны А, страница 46

Положение главного максимума  однозначно определяется из выражения (2):

Для определения ширины главного луча () в общем случае (при произвольном значении угла ) воспользуемся соотношением (3). При этом после ряда преобразований для ширины отклоненного луча получаем формулу

Дифракционные максимумы, как уже было отмечено, могут возникнуть в тех случаях, когда расстояние между соседними излучателяvи решетки 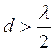.  Углы , соответствующие дифракционным максимумам, можно найти при помощи соотношения

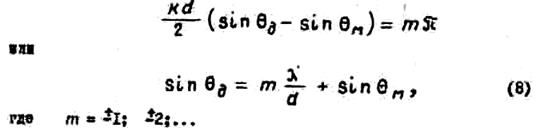
Ближайший к нормали дифракционный максимум будет иметь место при m= -I.  В этом случае из выражения (8) получим, что

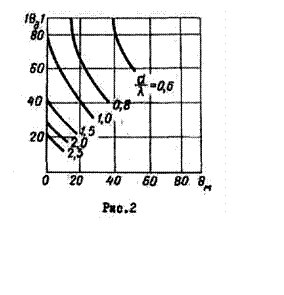
Направление дифракционных максимумов  и их число зависят от длины волны  расстояния между соседними излучателями в решетке d и направления главного максимума  (рис.2).

Если 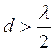 то, дифракционные максимумы отсутствуют при нюбых положениях главного максимума . Очевидно также, что при поперечном излучении (=0) дифракционные максимумы могут возникнуть лишь в случае, если расстояние между соседними излучателями . Как видно из рис.2, при = 0,6  дифракционный максимум появится, когда  превысит 40°, а при  =0,8, когда  большим 13°. В тех случаях, когда , дифракционные максимумы имеют место при любых положениях главного максимума.

Следует подчеркнуть, что дифракционные максимумы, интенсивность

которых близка к интенсивности главного максимума, совершенно недопустимы в большинстве применяемых антенных решеток. Поэтому, если решетка составлена из излучателей, направленные свойства которых близки к изотропным (например, полуволновые вибраторы в плоскости Н или полуволновые щели в плоскости E), расстояние между центрами соседних излучающих элементов следует выбирать не больше чем . Это в свою очередь приводит к необходимости использования для создания остронаправленных диаграмм сравнительно большого числа излучателей и соответственно большого числа распределительных и управляющих устройств.

Длина решетки L определяется требуемой шириной луча () и может быть найдена для неотклоненного луча при помощи соотношения (4), а для отклоненного - при помощи формулы (7).

Уменьшить число излучателей в решетке (при сохранении неизменной ширины луча) можно увеличением расстояния между ними, а для подавления возникающего при этом дифракционного лепестка следует использовать направленные излучатели.

Излучатели, диаграммы направленности которых можно приближенно аппроксимировать функцией вида cos условимся называть слабонаправленными. К их числу будем относить полуволновые вибраторы (в плоскости E ), полуволновые щели (в плоскости Н ), излучатели в виде открытых концов волноводов и рупоры с небольшими раскрывали ().

В нашем случае для анализа удобно записать диаграмму направленности решетки в виде

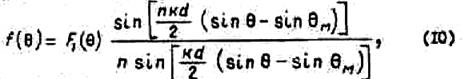
где     F₁()=cos- ДН излучателя решетки.

Если в выражение (10) подставить =, то получим (в относительном масштабе) амплитуду, соответствующую главному максимуму, а подстановка  =, даст значение амплитуды, соответствующее дифракционному максимуму в том же масштабе. Проделав эти операции, получим соответственно, что f() = соs, a f() = cos. Таким образом, отношение амплитуды дифракционного максимума f() амплитуде главного максимума можно представить формулой

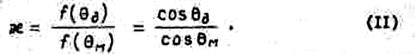
На рис.3 показаны зависимости  от углового положения главного максимума  для фиксированных значений расстояния между соседними излучателями . При этом для определения соответствия между углами  и , естественно, использовалась формула (9).

Итак, по мере отклонения луча от направления нормали к решетке (с ростом угла ) максимума   в соответствии с уменьшением значения функции

определяющей ДН излучателя решетки. Наряду с этим при каком-то значении угла  (оно определяется расстоянием между соседними излучателями  )  в направлении, характеризуемом углом , появляется дифракционный лепесток, максимум которого возрастает при дальнейшем росте угла . Как амплитуда главного максимума, так и амплитуда дифракционного определяются одной и той же функцией , только в первом случае значение ее следует рассчитать для  угла  =, а во втором - дня угла  =.