Основные электрические параметры антенн. Эффективная площадь антенны А, страница 6

В выражении (5) первый множитель представляет собой ДН одиночного излучателя, а второй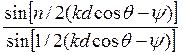

является множителем решетки . Он не зависит от свойств одиночного излучателя и полностью определяется параметрами решетки .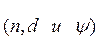

Таким образом, выражение для ДН линейной решетки идентичных излучателей можно представить в виде

Из выражения (5) видно, что ДН изотропных излучателей определяется множителем решетки, т.е.

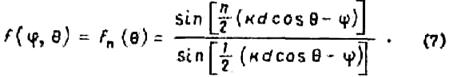
Следствием соотношений (5), (6) и (7) является теорема перемножения ДН:

ДН линейной решетки идентичных излучателей определяется произведением ДН одиночного излучателя на ДН той же линейной решетки воображаемых точечных изотропных излучателей.

Множитель  представляет собой ненормированную ДН линейной решетки из  изотропных ненаправленных излучателей:

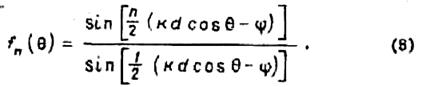
В направлениях , для которых суммарный сдвиг по фазе  имеет место арифметическое сложение полей и множитель решетки приобретает максимальные значения. Если , то выражение (8) дает неопределенность вида . Раскрытие ее по правилу Лопиталя приводит к значению .  Действительно,

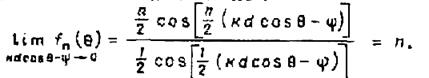
Следовательно, при  имеет место максимум множителя решетки. Нормированное выражение для  приобретает поэтому вид

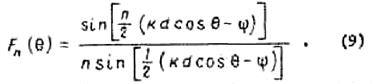
Используем полученные выражения для исследования некоторых типов антенных решеток.

Два ненаправленных излучателя. При  выражение (8) приобретает вид

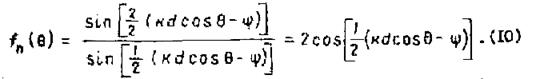
Эта формула определяет ДН двух ненаправленных излучателей, разнесенных на расстояние , с токами, сдвинутыми по фазе на угол . В частности, это может быть ДН в горизонтальной плоскости для двух вертикальных вибраторов.

Рассмотрим несколько частных случаев.

1. Два синфазных ненаправленных излучателя на расстоянии

При этом

Выражение обращается в нуль при   и  и имеет максимум при  . Результирующая диаграмма направленности изображена на рис.2,а.

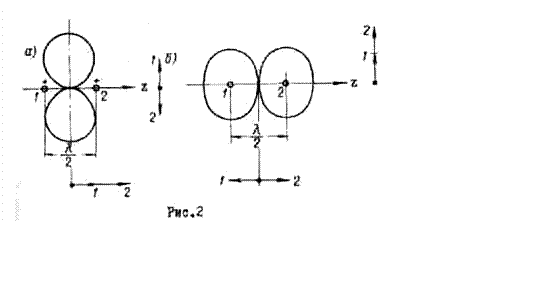
Рассмотренная антенная система характеризуется тем, что максимумы излучения получаются в направлении, перпендикулярном линии расположения излучателей, так как в этом направлении длина пути от каждого излучателя до точки наблюдения будет одинаковой. Поэтому векторы напряженности полей, создаваемых каждым из вибраторов, будут складываться в фазе. Минимумы излучения (нули) получаются вдоль линии расположения излучателей. Это объясняется тем, что поля, излучаемые двумя синфазными источниками, в рассматриваемом направлении проходят пути, отличающиеся между собой на половину длины волны. В результате волны, попадающие в точку наблюдения, оказываются в противоположных фазах.

2. Два противофазных ненаправленных излучателя на расстоянии 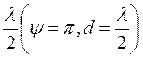. В этом случае

Выражение обращается в нуль при     и имеет максимум при     и . Диаграмма направленности, соответствующая этому случаю, изображена на рис.2,б.

3. Два ненаправленных излучателя на расстоянии   при произвольном фазовом сдвиге между токами . В этом случае ДН определяется выражением (10), главный максимум занимает промежуточное положение (рис.3) между случаями    и   , a угол    ему соответствующий, можно найти при помощи соотношения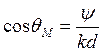         

4. Два ненаправленных излучателя при большом расстоянии между ними . Здесь мы рассмотрим синфазные и противофазные излучатели.

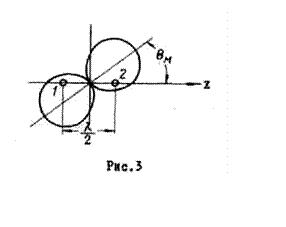
В первом случае возрастание расстояния между излучателями приводит к увеличению числа лепестков, а сами лепестки становятся более острыми. Однако при этом максимум одного из лепестков, ориентированный перпендикулярно линии расположения излучателей, не меняет своего положения. На рис.4 сплошными линиями показана ДН при расстоянии между излучателями . Направления максимумов и нулей можно определить, пользуясь выражением

Из последней формулы в результате несложных преобразований можно получить значения углов , соответствующих направлениям максимумов, в виде соотношения

и значения углов , соответствующих нулевым направлениям,

Во втором случае (при противофазном питании излучателей) максимумы и нули в ДН меняются местами

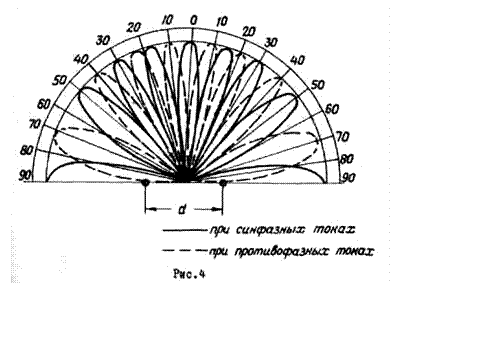
(пунктирные линии на рис.4). При этом нулевые направления определяются формулой

а направления максимумов