Основные электрические параметры антенн. Эффективная площадь антенны А, страница 8

При достаточно большом числе элементов  каждый из них можно считать элементарным диполем и поэтому положить, что

Множитель решетки определяется формулой (9). Его удобно записать в виде 

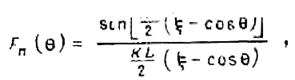
где 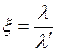 - коэффициент укорочения волны в проводе.

Таким образом, общее выражение для нормированной ДН провода с бегущей волной приобретает вид    

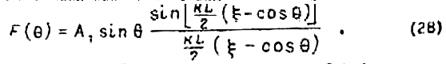
На рис.10 показаны: ДН элементарного диполя, множитель решетки и  результирующая ДН провода с бегущей волной тока . Главный максимум в результирующей ДН ориентирован под некоторым острым углом к оси провода.

КОЭФФИЦИЕНТ НАПРАВЛЕННОГО ДЕЙСТВИЯ АНТЕНН

Теперь, пользуясь исходным выражением [тема 1, формула (9)] , получим выражения для расчета коэффициента направленного действия (к.н.д.) антенн.

Окружим антенну сферой большого радиуса. Поток мощности через элемент  поверхности сферы

где      - действующее значение напряженности поля на элементе

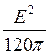 - плотность потока мощности в свободном пространстве ( численное значение вектора Пойнтинга).

Мощность излучения любой антенны может быть найдена как gjток мощности через всю поверхность сферы, т.е. как

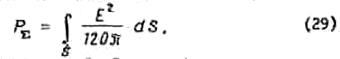
Для ненаправленной антенны  независимо от направления и

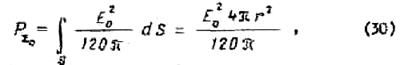
где  - площадь поверхности сферы.

Напряженность поля направленной антенны

где   напряженность поля в направлении максимума ДН антенны, а  - нормированная ДН. Поэтому для направленной антенны мощность излучения

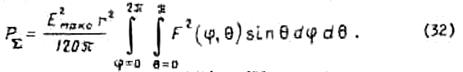
Взяв отношение выражения (30) к (32), получаем

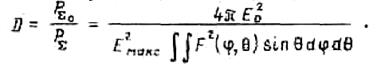
Из данного выше определения коэффициента направленного действия следует, что напряженность поля ненаправленной антенны равна напряженности поля в направлении максимума направленной антенны, т.е. что . Поэтому

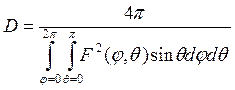                     (33)

Это и есть общее выражение для расчета коэффициента направленного действия антенны в  направлении  главного  максимума  по заданной нормированной диаграмме.

Коэффициент направленного действия в любом направлении  можно найти при помощи соотношения

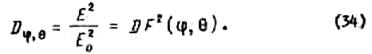
Последнее выражение свидетельствует о том, что зависимость к.н.д. от направления совпадает по форме с ДН антенны по мощности.

Выведем еще одно выражение, удобное для расчета к.н.д. линейных антенн, напряженность поля которых можно представить в виде

где  - нормированная ДН антенны.

Мощность излучения антенны при этом

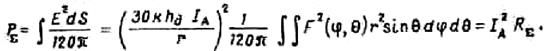
Поэтому сопротивление излучения антенны  можно выразить через ее ДН следующим образом:

Из формулы (33) следует, что

поэтому

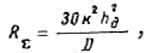
откуда

Для расчета коэффициента направленного действия антенн сверхвысоких частот (рупорных, зеркальных и некоторых других) используется выражение

где    - эффективная площадь антенны.

Часто коэффициент направленного действия антенн выражают и децибелах:

Такая запись особенно удобна для остронаправленных антенн, к.н.д. которых достигает значений .

Между коэффициентом направленного действия антенны и углами раствора диаграмм направленности в двух главных взаимно перпендикулярных плоскостях существует определенная связь. Покажем ее на примере антенны с прямоугольным раскрывом, во всех точках которого поле одинаково как по амплитуде, так и по фазе.

С помощью выражения (38) легко получить следующую формулу:

где  и  - размеры сторон прямоугольного раскрыва.

Углы раствора диаграмм направленности в плоскостях, параллельных сторонам  и , на основании равенства (25) определяются выражениями                                                                                    

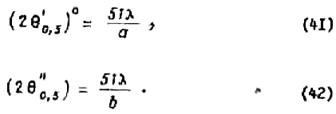
Подставляя значения  и  из выражений (41)  и (42) в  (40), получаем, что

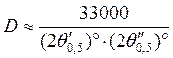           (43)

В случае квадратного раскрыва, когда углы раствора диаграммы в двух взаимно перпендикулярных плоскостях равны,

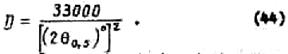
Коэффициент, стоящий в числителе выражений (43) и (44), может меняться в довольно широких пределах. Так, для антенн с большим уровнем боковых лепестков в диаграмме направленности он уменьшается до величины порядка 15000 - 20000. Наоборот, для зеркальных антенн, уровень боковых лепестков которых сравнительно невелик, этот коэффициент возрастает до величины 35000 - 40000.