Основные электрические параметры антенн. Эффективная площадь антенны А, страница 7

Линейная решетка из  ненаправленных излучателей. Нормированная ДН такой решетки в общем случае определяется выражением (9).

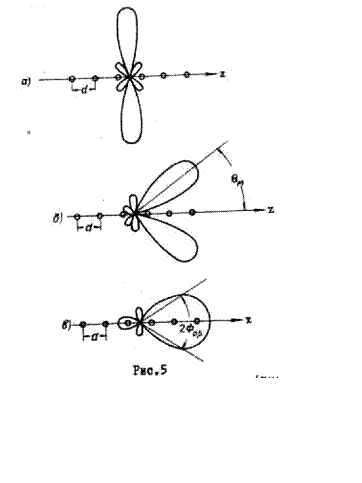
Если сдвиг по фазе между токами в соседних излучателях , то имеет место поперечное излучение (главный максимум перпендикулярен к линии расположения излучателей - рис.5,а).

          В случае, когда , главный максимум ориентирован вдоль линии расположения излучателей (рис.5,в), и излучение называется продольным. Если сдвиг по фазе соответствует промежуточному значению , то главный максимум расположен под углом  к линии расположения излучателей (рис.5,б). Этот угол определяется равенством                    

Если излучатели синфазны , то ДН определяется соотношением

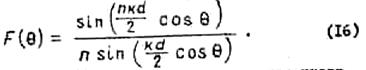
Нулевые направления  можно найти, приравняв нулю числитель выражения (16), но при этом знаменатель не должен обращаться в нуль. Математически это можно записать в виде

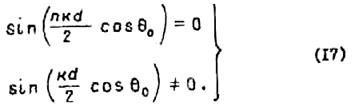
Из формулы (17) получаем, что

Типичная ДН для случаев, когда , показана  на рис.6. Она состоит из одного главного лепестка (максимум его перпендикулярен оси ) и ряда боковых меньшей интенсивности. В такой решетке точно определяются нулевые направления при помощи соотношения (18).

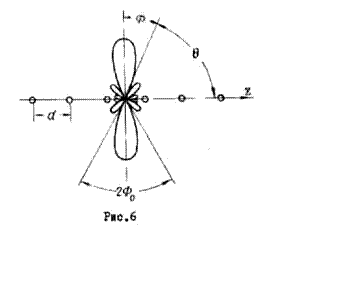При анализе удобно отсчет углов производить не от оси , а от направления, перпендикулярного этой оси. При таком отсчете углов (рис.6) выражение (16) приобретает вид

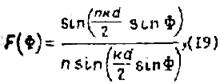
где - угол, отсчитываемый от направления главного максимума.

Направление , соответствующее нулю главного лепестка, можно найти из выражения (18). При  имеем

Если число излучателей достаточно велико , то  главный лепесток получается острым и тогда можно воспользоваться приближенным соотношением

Таким образом, угол раствора главного лепестка ДН по нулевым значениям  (рис.6) определяется формулой

Ширину ДН на уровне половинной мощности можно определить, пользуясь выражением (19). При этом справедливым оказывается равенство

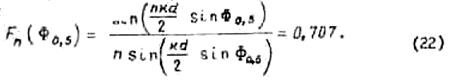
В общем случае уравнение (22) может быть разрешено графическим путем.

Однако если число излучателей достаточно велико, то в знаменателе в пределах главного лепестка синус можно заменить его аргументом. Тогда из выражения (19) получим

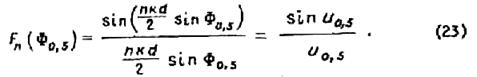
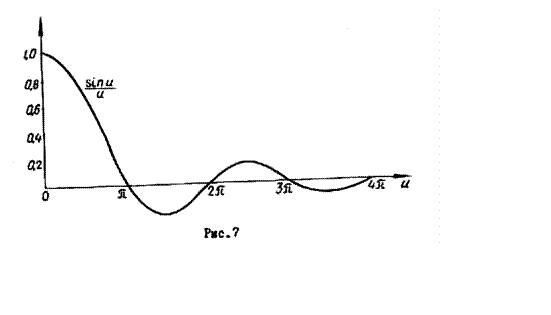На рис.7 приведен график функции , где 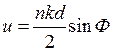. Отсчитывая на нем ординату, соответствующую уровню 0,707, находим абсциссу .

Таким образом, можем записать равенства

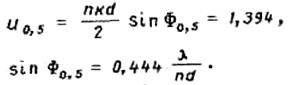
При достаточно большом числе излучателей длина антенны ,  а ДН острая, поэтому

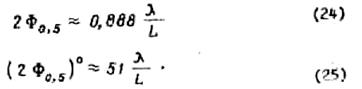
Если расстояние между соседними излучателями мало , то ДН описывается выражением

где    

Соотношение (26) называется обобщенной ДН линейной решетки излучателей.

Диаграмма направленности двух полуволновых симметричных вибраторов. Как уже было показано, ДН решетки направленных излучателей определяется выражением (6). Отсюда видно, что ДН решетки можно получить путем умножения ДН полуволнового вибратора (см.тема 4,рис.6) на множитель решетки: .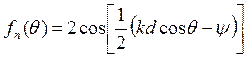

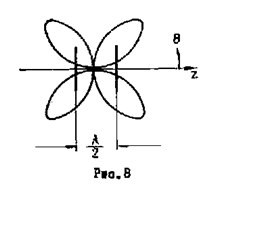На рис.8 в качестве примера показана ДН двух синфазных полуволновых вибраторов при расстоянии между ними 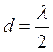. Она получена в результате умножения диаграммы рис.2,а на ДН полуволнового вибратора.

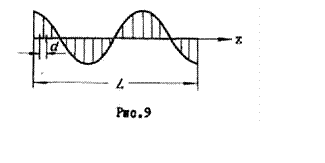
Излучатель в виде провода с бегущей волной тока. Рассмотрим провод длиной  (рис.9) с бегущей волной тока. Выражение для тока, если волна бежит слева направо, имеет вид

где   - ток в начале провода;

здесь   - длина волны в проводе.

Разделим провод на большое число одинаковых элементов . При этом длина каждого элемента 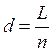, а расстояние между их центрами также оказывается равным . Ток в каждом последующем элементе отстает по фазе от тока в предыдущем на угол . ДН всего провода можно записать как ДН решетки из  направленных излучателей, т.е. в виде соотношения

где      - угол, отсчитываемый от оси провода;

- нормирующий множитель (его введение необходимо потому, что направления максимумов для множителей  и  в общем случае не совпадают);

  -  ДН элемента провода;

 - ДН линейной решетки из  ненаправленных излучателей, разнесенных на расстояние  друг от друга, с токами, сдвинутыми по фазе на угол .