Физика \ Физико-химические основы и элементы технологии процесса нанесения вакуумных покрытий

Ионно-плазменная технологическая установка для нанесения защитно декоративного покрытия на изделия широкого потребления, страница 11

Рабочее вещество, предназначенное для напыления поверхности, попадает в технологическую камеру через канал подачи рабочего газа, который аналогичный каналу подачи рабочего вещества в ускорительный блок, а далее направляется в МРС (18).

Реагентный газ азот (14) поступает в технологическую камеру по каналу подачи реагентного газа, который аналогичный каналам подачи рабочего газа для очистки поверхностей изделий и осаждения покрытия. Пройдя канал подачи реагентного газа, азот поступает на коллекторы.

2.6 Расчет на прочность крышки вакуумной камеры

Рассчитаем на прочность верхнюю крышку вакуумной камеры, расчет проводим по методике [17].

При расчете примем крышку оболочкой. Под оболочкой понимают тело, у которого одно из трех измерений значительно меньше двух других.

На крышку вакуумной камеры действуют: распределенная нагрузка – разность давлений внутри и снаружи камеры (р=105 Па); концентрированные нагрузки – вес катодного узла магнетронной (R1=1500Н) системы распыления. Действующая нагрузка показана на рисунке 2.6.

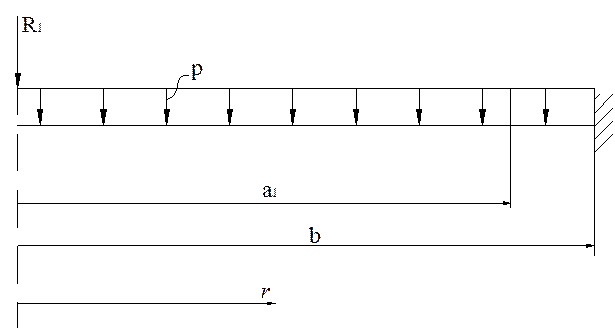
Рисунок 2.6 Схема действия нагрузок на крышку вакуумной камеры

В расчете на прочность крышки камеры учитываем только изгибающий момент от действующих нагрузок.

Для определения напряжений, возникающих при изгибающем моменте, определим прогиб крышки от действующих нагрузок.

ω=ω1+ω2+ω3,                                                                       (2.119)

где ω, ω1, ω2, ω3 – суммарный прогиб крышки и прогибы крышки от нагрузок R1, R2 и р соответственно.

Прогиб пластины под действием концентрированной нагрузки определяется по формуле:

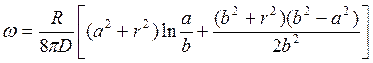,                         (2.120)

где R – действующая нагрузка, D – цилиндрическая жесткость, а – расстояние от центра пластины до точки приложения нагрузки, b – радиус пластины,

r – текущий радиус рассматриваемого сечения.

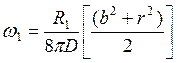,                                      (2.121)

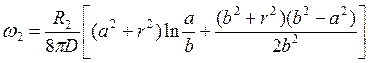.                          (2.122)

Прогиб крышки под действием распределенной нагрузки:

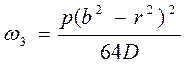.                                               (2.123)

Для рассматриваемой крышки a=0.6 м, b=0.7м, R1=1500 Н, R2=3000 Н, р=105 Па.

После соответствующих подстановок формула (2.31) примет вид:

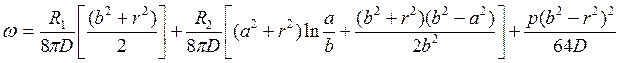     (2.124)

Для определения напряжений найдем вторую производную прогиба по координате r :

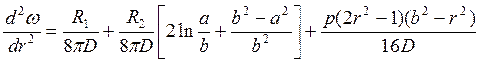.        (2.125)

Напряжение в крышке определим по формуле:

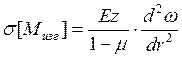,                                      (2.126)

где E=2.2·105 МПа – модуль Юнга,

μ=0.3 – коэффициент Пуассона.

Цилиндрическая жесткость определяется по формуле:

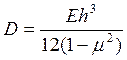.                                               (2.127)

Подставив полученные значения в формулу (2.124) и (2.126) получим функцию изменения прогиба и напряжения в крышке по расстоянию от осевой линии до рассматриваемого сечения. Расчеты проведены с помощью программы MathCAD, полученные результаты представлены в таблица 2.1. Графики зависимости представлены на рисунках 2.7 и 2.8.

Таблица 2.1 Зависимость величины прогиба крышки и напряжения в ней от радиуса рассматриваемого сечения крышки

r, м

0

0,1

0,2

0,3

0,4

0,5

0,55

0,6

0,65

0,67

0,7

ω, мм

4,04

3,9

3,5

2,88

2,15

1,42

1,15

0,875

0,47

0,3

0

σ, МПа

69,5

67

58,5

46,1

31,2

16

9,4

4

0,25

-0,65

-1,26

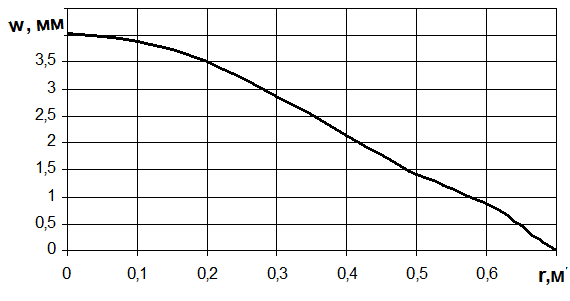
Рисунок 2.7 График зависимости величины прогиба под действием от нагрузок от радиуса рассматриваемого сечения.

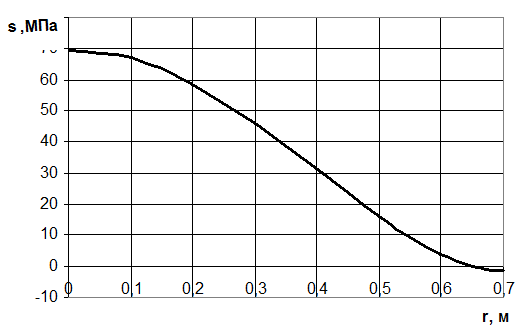
Рисунок 2.8 График зависимости напряжений от действующих нагрузок от радиуса рассматриваемого сечения.

Очевидно, что максимальное значение напряжения в центре крышки камеры и составляет 69.5 МПа.

Коэффициент запаса прочности можно определить по формуле:

,

(2.128)
Скачать файл