Создание обучающей системы автоматизированного проектирования маломощных электромеханических следящих систем, страница 23

Передаточную функцию разомкнутой нескорректированной системы обычно можно записать в виде:

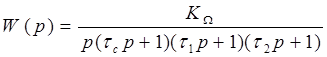,                                                       (5)

где     K_Ω  – добротность системы по скорости,

 – постоянная времени двигателя с учетом нагрузки на валу,

 – постоянная времени усилителя,

 – постоянная времени фильтра.

Постоянная времени двигателя с учетом нагрузки на валу равна:

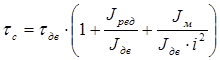,                                                    (6)

Коэффициент передачи K_Ω (добротность) нескорректированной разомкнутой системы является варьируемым параметром (его можно менять, изменяя коэффициент передачи усилителей) и определяется исходя из обеспечения заданной динамической точности (скоростной ошибки q_дmax) по формуле:

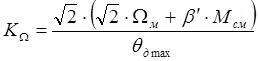,                                              (7)

где β´ – коэффициент наклона механической характеристики двигателя, приведенный к валу механизма:

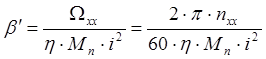,                                             (8)

2.3.10 Синтез желаемой ЛАХ

Наиболее удобным и наглядным методом синтеза систем автоматического регулирования является метод логарифмических амплитудных характеристик. Этот метод применим только для минимально-фазовых систем.

Формирование желаемой ЛАХ в низкочастотной области определяется требованием обеспечения заданной точности в виде максимальной ошибки q_max в гармоническом режиме работы.

Требование к низкочастотной области ЛАХ формулируется следующим образом: для того чтобы входное воздействие воспроизводилось с суммарной ошибкой q_дин не больше q_дmax, ЛАХ системы должна проходить не ниже контрольной точки A_к с координатами:

ω = ω_к,    L(ω_к) = 20·lg|W(jω_к)| = 20·lg(K_Ω/ω_к),

Область, расположенная ниже контрольной точки A_к и двух прямых с наклонами –20 и –40 дБ/дек, представляет собой запретную область для ЛАХ следящей системы любого порядка. При работе со скоростями и ускорениями, не превышающими W_мmax и e_мmax, ошибки следящей системы не будут превосходить значения q_дmax, если ЛАХ будет проходить не ниже запретной области.

Формирование ЛАХ в области средних частот (в окрестности частоты среза ω_ср) подчинено требованию обеспечения заданного значения показателя колебательности М. Для того чтобы система имела показатель колебательности не выше М, ее фазочастотная логарифмическая характеристика должна проходить вне запретной области. Это условие выполнится в том случае, если ЛАХ системы пересекает ось нуля децибел на участке с наклоном –20 дБ/дек и границы этого участка удовлетворяют условиям:

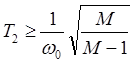,                                                                   (9)

сумма постоянных времени правее частоты среза:

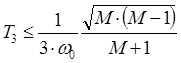,                                                 (10)

где  –  частота среза,, .

2.3.11 Определение структуры и электрической схемы КУ

Задача выбора корректирующих устройств по заданным требованиям к желаемой ЛАХ не решается однозначно. Одни и те же ЛАХ W_ск(p) могут быть обеспечены различными корректирующими устройствами. С практической точки зрения все эти возможные варианты реализации желаемой ЛАХ существенно отличаются друг от друга. Система с различными корректирующими связями, обеспечивающими одинаковую ЛАХ W_ск(p), имеют различную чувствительность к внутренним сигналам помех и нелинейностям, а также отклонениям ее параметров. Поэтому вначале рассматривают все варианты коррекции системы, а в дальнейшем выбирают из них наиболее рациональный.        

Проще всего реализовать последовательное КУ, работающее на постоянном токе, включив его между демодулятором и модулятором. Передаточную функцию последовательного  корректирующего устройства  можно определить из соотношения:

W_ск(p) = W_ку(p)· W_исх(p).                                                    (11)

2.3.12 Схемотехническая реализация СС

Для выполнения данного этапа курсового проекта студентам кафедры И3 рекомендуется воспользоваться курсовым проектом по дисциплине «Схемотехника», выполненным курсом ранее согласно учебному плану. Данный подраздел пособия иллюстрирует пример расчета (по сути продолжающий пример, рассмотренный в п.2.2).