Лабораторная работа № 1
ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы - сравнительный анализ различных методов повышения точности САУ.
1. Основные сведения из теории
К числу важнейших показателей качества систем автоматического управления (САУ) относится установившаяся (статическая) ошибка – величина ошибки регулирования x(t)=g(t)-y(t) в установившемся процессе. Здесь g(t) – задающее воздействие, y(t) – выход системы.
Установившаяся ошибка САУ может быть измерена по окончании переходного процесса или рассчитана. Для линейной системы при известных структуре, параметрах и задающем воздействии используется теорема о конечном значении:
![]() , где
Фx(s)
– передаточная функция замкнутой системы
по ошибке, G(s) - изображение
по Лапласу задающего воздействия.
, где
Фx(s)
– передаточная функция замкнутой системы
по ошибке, G(s) - изображение
по Лапласу задающего воздействия.
При одновременном действии на систему нескольких сигналов используется принцип суперпозиции:
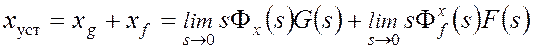 , (1)
, (1)
где
xg, xf-
составляющие статической ошибки, определяемые задающим и возмущающим
воздействиями; ![]() - передаточная функция замкнутой
системы по ошибке от возмущающего воздействия; F(s) - изображение по Лапласу возмущающего воздействия f(t).
- передаточная функция замкнутой
системы по ошибке от возмущающего воздействия; F(s) - изображение по Лапласу возмущающего воздействия f(t).
Если главная обратная связь в системе единичная и отрицательная, соотношение (1) принимает вид
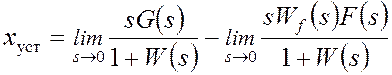 , (2)
, (2)
где W(s) - передаточная функция разомкнутой системы, Wf (s) - передаточная функция разомкнутой системы по возмущающему воздействию.
Если система является статической как по задающему, так и по возмущающему воздействиям, то при g(t)=g01(t)и f(t)=f01(t) формула (2) позволяет получить
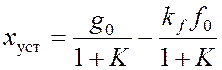 ,
(3)
,
(3)
где K - общий коэффициент усиления по разомкнутой цепи, kf - коэффициент передачи от точки приложения возмущения f(t) до выхода системы y(t).
Из выражения (3) следует, что величина ошибки статической системы может быть уменьшена при увеличении общего коэффициента усиления. Однако это увеличение связано с уменьшением запасов устойчивости системы. Поэтому одновременно с увеличением коэффициента K необходимо вводить в САУ корректирующие (демпфирующие) средства.
Разработаны и другие методы повышения точности:
1) повышение порядка астатизма, что соответствует введению в систему интегрирующих или изодромных звеньев;
2) введение производной от ошибки в закон регулирования;
3) введение неединичных обратных связей;
4) применение комбинированного регулирования.
1.1. Описание исследуемой системы
В работе исследуется система управления, структурная схема которой изображена на рис.1. Нескорректированная система состоит из трех последовательно включенных апериодических звеньев. К системе приложено задающее воздействие g(t)=g0×1(t), на объект управления также действует возмущающее воздействие f(t)=f0×1(t).
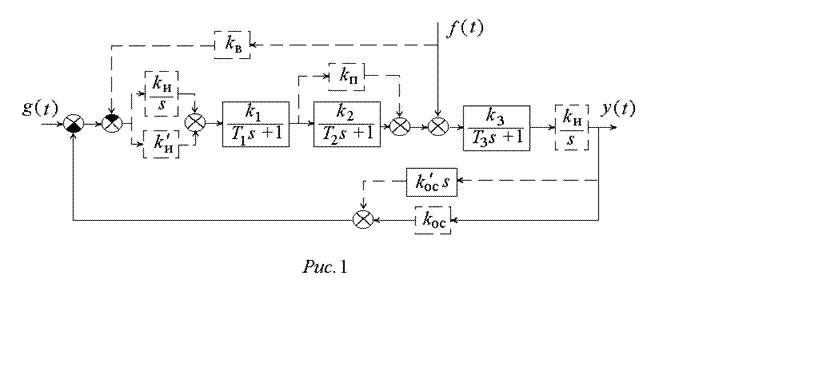 |
1) прямое параллельное корректирующее устройство с коэффициентом передачи kп , позволяющее ввести производную от ошибки в закон регулирования;
2) вспомогательное дифференцирующее звено с коэффициентом передачи k'ос, позволяющее реализовать гибкую обратную связь;
3) интегрирующее звено с коэффициентом передачи kи, позволяющее повысить порядок астатизма системы;
4) изодромное звено с коэффициентами передачи kи и k'и, позволяющее повысить порядок астатизма системы без существенной потери запаса устойчивости;
5) вспомогательное звено с коэффициентом передачи kос, позволяющее реализовать цепь основной обратной связи с коэффициентом передачи, отличным от единицы;
6) дополнительное звено с коэффициентом передачи kв, позволяющее вводить на вход системы сигнал, пропорциональный возмущению f(t), с целью компенсации последнего, и тем самым создать комбинированную систему управления.
1.2. Нескорректированная система
Исходная система является статической и состоит из трех последовательных апериодических звеньев, охваченных единичной обратной связью (kос=1). Передаточная функция разомкнутой системы
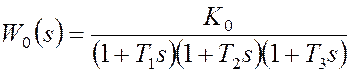 , где K0=k1k2k3 - общий коэффициент усиления.
, где K0=k1k2k3 - общий коэффициент усиления.
Основная передаточная функция нескорректированной замкнутой системы:
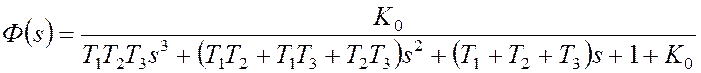 . (4)
. (4)
Характеристический полином нескорректированной замкнутой системы:
![]() .
.
Используя критерий устойчивости Гурвица, можно определить условия устойчивости замкнутой САУ и критическое значение коэффициента K0, при котором нескорректированная САУ будет находиться на колебательной границе устойчивости.
В случае характеристического полинома третьей степени для анализа устойчивости достаточно рассмотреть определитель второго порядка:
![]() .
.
Условием устойчивости является неравенство D2>0, откуда
K0<K0кр , где 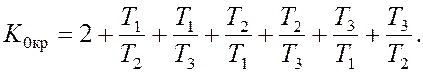
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.