Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 3

Отметим, что от места включения в систему изодромного звена зависит достижение астатизма по всем или части воздействий, что полностью аналогично результатам предыдущего  пункта.

1.7. Введение неединичной обратной связи

В данной работе неединичная обратная связь реализуется путем введения в цепь главной обратной связи дополнительного звена с коэффициентом передачи k_oc (см. рис.1).

В этом случае передаточная функция замкнутой системы автоматического регулирования определяется следующим образом:

.

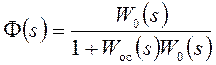Для получения полной инвариантности САУ по отношению к задающему воздействию необходимо выполнение условия Ф(s)=1, откуда следует требуемая передаточная функция главной обратной связи:

.

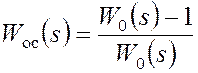Реализация частичной инвариантности (обеспечение астатизма первого порядка относительно задающего воздействия) достигается жесткой обратной связью с коэффициентом передачи:

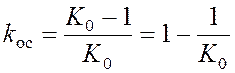.                                      (10)

Если возмущающее воздействие f(t) будет приложено к САУ, то установившееся значение ошибки определяется лишь составляющей x_f , вызванной возмущающим воздействием.

Из вышеизложенного следует, что введение неединичной обратной связи позволяет обеспечить астатизм по задающему воздействию для исходной статической САУ.

1.8. Комбинированное регулирование

Использование рассмотренных выше методов повышения точности САУ вызывает  общие трудности, связанные с обеспечением устойчивости системы и надлежащего качества переходных процессов.

Поэтому при решении задачи повышения точности САУ иногда целесообразно отойти от чистого принципа регулирования по отклонению (или по интегралам и производным от него) и соединить этот принцип с другим - с регулированием по возмущающему или задающему воздействию. Такого рода системы регулирования называются комбинированными. В подобных системах регулирование осуществляется по замкнутому и разомкнутому контурам.

В данной лабораторной работе исследуется введение дополнительного регулирования по возмущению (см. рис.1). В соответствии со структурной схемой составляющая ошибки от возмущения может быть найдена из следующей системы уравнений в изображениях:

,  .

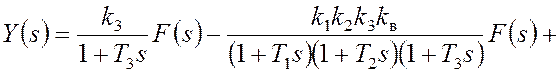
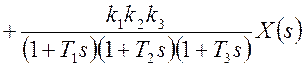Пусть g(t)=0 , тогда X(s) = -Y(s). Составляющая ошибки от возмущения определяется выражением

.

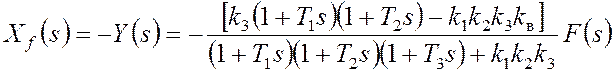Отметим, что характеристический полином комбинированнной системы остается без изменений, следовательно, введение регулирования по возмущению не влияет на устойчивость.

Установившаяся ошибка от возмущающего воздействия

.

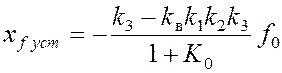При выполнении условия

k_вk₁k₂ = 1                                                    (11)

установившаяся ошибка обращается в ноль, то есть в системе достигается частичная инвариантность по отношению к возмущающему воздействию (система приобретает астатизм первого порядка). Рассмотренный прием по существу обеспечивает компенсацию ступенчатого возмущающего воздействия.

2. Порядок выполнения работы

Номер варианта в соответствии с табл.1 и перечень выполняемых разделов задаются преподавателем. Раздел А выполняется обязательно.

Исследование точности производится путем моделирования в среде MATLAB 5.*/SIMULINK [2].

Таблица 1

Варианты заданий

№ варианта	k1	k2	k3	T1	T2	T3	kп	k'ос	k'и
1	0,5	2	10	0,1	0,5	1	0,3	0,05	1
2	0,6	2	10	0,1	0,1	1	1	0,1	0,1
3	2	5	1	0,2	0,1	1	6	0,1	0,2
4	0,7	4	2	0,2	0,5	1	0,5	0,1	0,1

А. Исследование исходной нескорректированной системы

1. Запустить SIMULINK из MATLAB 5.0. C помощью технологии “drag-and-drop” (перетащи и оставь) построить модель исходной нескорректированной системы в соответствии с рис. 1 (звенья, показанные пунктиром, отсутствуют, обратная связь единичная).