Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 16

На практике из-за неидеальности элементов и дополнительных инерционностей в системе возникает движение с относительно высокой частотой и малой амплитудой относительно поверхности разрыва – так называемый реальный скользящий режим [2].

Рассмотрим поведение системы в идеальном скользящем режиме. Будем предполагать, что указанными факторами можно пренебречь и движение происходит непосредственно по поверхности переключения, а не в ее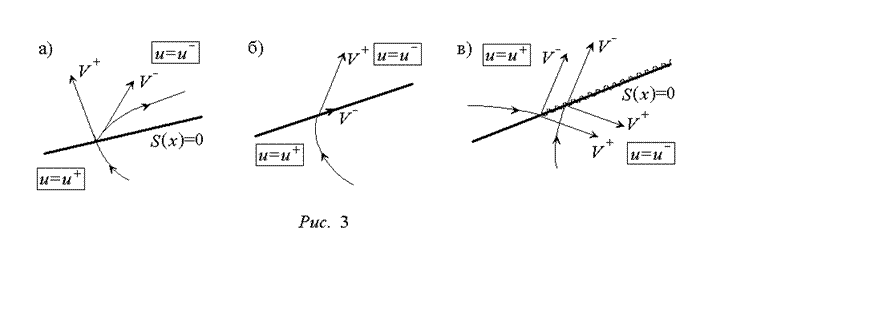
пограничном слое.

При теоретическом изучении скользящих режимов имеются определенные сложности, связанные с невыполнением условий теоремы существования и единственности решений дифференциальных уравнений. Дело в том, что правые части уравнений, описывающих процесс в СПС, претерпевают разрыв при переключении структур. Кроме того, как показано выше, в скользящем режиме изображающая точка находится на поверхности разрыва в каждый момент времени. Поэтому требуется доопределить уравнения системы таким образом, чтобы получить решение, описывающее движение по поверхности переключения, но без разрывов правых частей уравнения. Эта задача не может быть решена однозначно. Известно несколько способов такого доопределения [2].  Воспользуемся методом эквивалентного управления, предложенным В.И. Уткиным.

Пусть объект управления описывается системой уравнений

 ,                                            (1)

где X(t) - вектор состояния объекта, u(t) - управляющее воздействие.

Регулятор описывается зависимостью

u = j(X),                                                       (2)

причем функция  j(X) претерпевает разрыв на поверхности переключения, которая задается уравнением

S(X) = 0.                                                      (3)                                                                             

Это означает, что  при S(X) > 0 и  при S(X) < 0   а значение j⁰(X) при S(X) = 0 не определено.

Задача состоит в определении j⁰(X) таким образом, чтобы полученное непрерывное управление соответствовало движению системы по поверхности (3). Так как при таком движении S(X) = 0, то производная по времени функции  S(X),  вычисленная в силу системы (1), тождественно равна нулю, то есть

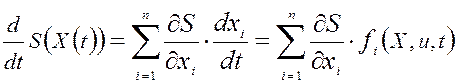 = 0.                    (4)

Из полученного соотношения (4) выразим эквивалентное управление  . Далее  подставляется в (1)  и  находится X(t) из совместного решения уравнений

, S(X) = 0.

Эквивалентное управление  имеет определенный физический смысл. Если рассмотреть движение системы (1), (2) в реальном скользящем режиме, то управление u(t) будет содержать колебания с высокой частотой. Если сигнал u(t) пропустить через фильтр с соответствующей постоянной времени, то можно выделить низкочастотную, или «среднюю», составляющую, которая и будет соответствовать [2].

В лабораторной работе рассматривается СПС, объект управления которой описывается системой уравнений

                                           (5)

где  a, b - параметры объекта, а управление u(t) обеспечивает попадание на поверхность разрыва вида (3) и движение по ней в скользящем режиме. Очевидно, для рассматриваемого объекта фазовое пространство представляет собой плоскость 0x₁x₂. Уравнение (3)  будем рассматривать в виде S(X) = tx₂ + x₁, где t - заданный параметр. Таким образом, поверхность разрыва в нашем случае – прямая на плоскости  0x₁x₂.

В соответствии с изложенным выше методом найдем  Имеем S(X(t)) = tx₂ + x₁,  , откуда в силу  (5)

.                                    (6)

Полагая , найдем :

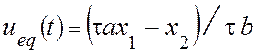 .                                      (7)

Подставив (7) в (5), получим систему уравнений, описывающих движение объекта в скользящем режиме:

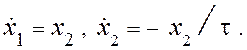                                       (8)

Уравнения (8) следует решать с учетом условия S(X) = tx₂ + x₁ = 0, откуда x₁ = -tx₂. Окончательное решение имеет вид

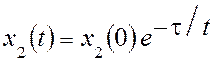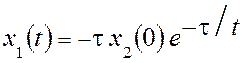, .                  (9)

Если задано x₁(0), нетрудно найти 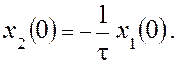 Отметим, что за начало отсчета времени здесь принят момент t^* возникновения скользящего режима.