Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 10

Из (1) и (7) получаем гармонически линеаризованное характеристическое уравнение замкнутой системы:

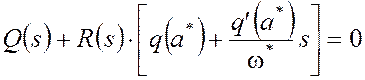,                              (8)

на основе которого определяется периодическое решение x^*=a^*sinw^*t (симметричные автоколебания) из условия нахождения системы на колебательной границе устойчивости, получаемого по критерию Михайлова:

или

                                    (9)

Если конечное решение уравнений (9) в области положительных вещественных чисел существует, соответствующие значения a^* и w^* являются параметрами предельного цикла для данной нелинейной системы. Возможны несколько решений и соответственно несколько предельных циклов.

Устойчивость предельного цикла может быть проверена по условию [1,2]

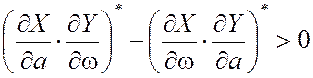.                                   (10)

Если для найденной пары (a^*,w^*) условие (10) выполняется и все коэффициенты полинома, входящего в уравнение (8), положительны, в системе возможны автоколебания с частотой w^* и амплитудой a^* на входе нелинейного звена.

В остальных случаях автоколебания в системе отсутствуют. Для системы выше четвертого порядка рассматриваются дополнительные условия [2].

Частотный способ определения автоколебаний основан на том, что в соответствии с критерием Найквиста колебательной границе устойчивости соответствует прохождение амплитудно-фазовой характеристики гармонически линеаризованной разомкнутой системы через точку (-1, j0). Следовательно, параметры возможных автоколебаний могут быть найдены решением уравнения

или

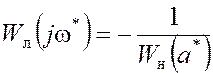.                                           (11)

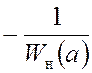На комплексной плоскости строятся годограф W_л(jw) для  и годограф функции  для . Точки их пересечения дают параметры возможных автоколебаний, после чего  применяются известные критерии устойчивости найденного периодического решения [1].

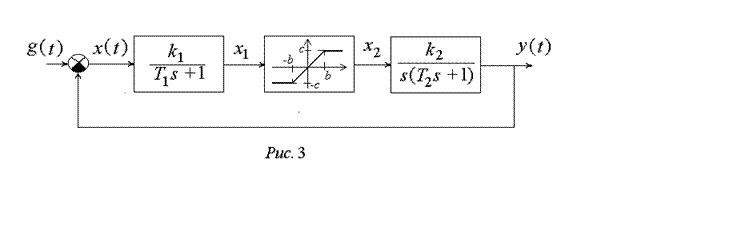
Рассмотрим САУ, структурная схема которой представлена на рис. 3.

Передаточная функция линейной части системы имеет вид

.

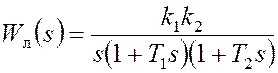Коэффициенты гармонической линеаризации нелинейности (рис. 4):

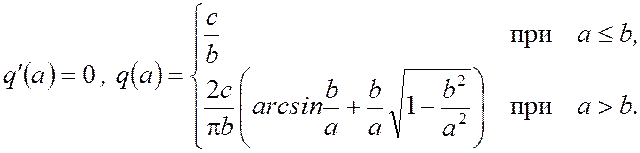
Уравнения (9) принимают вид

,

.

Из второго уравнения определим частоту периодического решения:

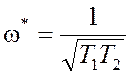, а из первого получаем

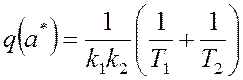,                                        (12)

откуда можно определить амплитуду периодического решения.

Проверку его устойчивости по критерию (10) предлагается провести самостоятельно.

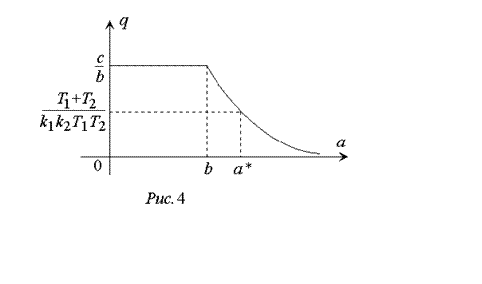
Отметим, что с учетом 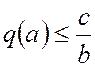 (рис. 4) уравнение (12) будет иметь решение только при

.

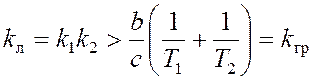При k_л < k_гр автоколебания в системе отсутствуют.

Теперь рассмотрим нелинейную САУ, структурная схема которой показана на рис. 5. Для этой системы коэффициенты гармонической линеаризации имеют вид

,

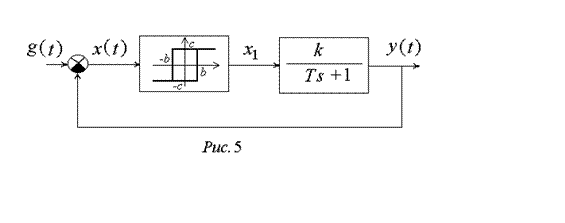
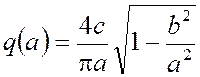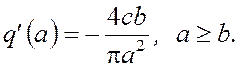
Автоколебания будем определять частотным способом.

Годограф данного нелинейного звена определяется функцией

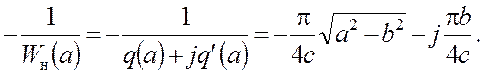
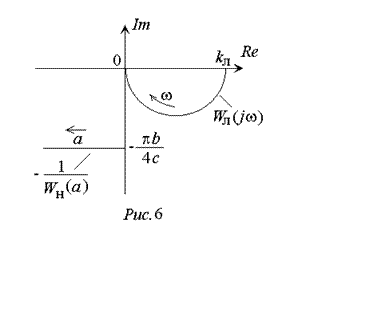
Из рис. 6 в соответствии с  частотным способом определения автоколебаний следует, что в рассматриваемой системе автоколебания невозможны при любых значениях параметров. Однако моделирование данной системы этот вывод не подтверждает.

Отсюда заключаем, что в некоторых случаях применение метода гармонической линеаризации приводит к качественно неверным результатам.

Приведенный пример подтверждает, что  метод гармонической линеаризации является приближенным в силу использования гипотезы о наличии у линейной части системы свойства фильтра. В частных случаях эта гипотеза может не подтвердиться даже при указанном выше соотношении степеней числителя и знаменателя передаточной функции линейной части. Поэтому после получения результатов на основе гармонической линеаризации целесообразна их расчетная или экспериментальная проверка.

Проверить наличие свойства фильтра у линейной части расчетным путем можно путем вычисления значений ее амплитудно-частотной характеристики для частот w^*, 2w^*, 3w^*, найденных рассмотренным выше способом , или путем моделирования системы.

Экспериментально наличие свойства фильтра может быть проверено путем подачи на вход линейной части разомкнутой системы гармонических сигналов с частотами w^*, 2w^*, 3w^* и измерения амплитуды выходного сигнала.