Одной из особенностей нелинейных систем является возможность возникновения автоколебаний. Автоколебания – это собственные незатухающие периодические колебания, параметры которых определяются внутренними свойствами системы. Возможность возникновения автоколебаний в конкретной системе может зависеть в общем случае от вида и параметров нелинейностей, структуры линейной части и значений отдельных параметров динамических звеньев системы (коэффициентов передачи, постоянных времени), а также от начальных условий.
Одним из наиболее широко распространенных методов исследования нелинейных систем является метод гармонической линеаризации. Он весьма удобен для определения условий возникновения автоколебаний и их параметров. В последнее время область его применения распространена на широкий класс задач исследований нелинейных систем (анализ вынужденных колебаний, определение показателей качества колебательных переходных процессов и др.).
Для системы с одной нелинейностью и произвольной структурой линейной части основные положения метода гармонической линеаризации состоят в следующем.
Пусть нелинейность выделена в отдельное звено со статической характеристикой y=F(x) и известна передаточная функция линейной части (рис.1):
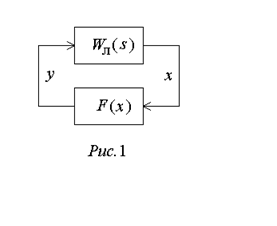
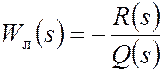. (1)
Если на входе нелинейного звена действует гармонический сигнал
x=asinwt, (2)
выходной сигнал звена является периодической функцией сложной формы, которая может быть разложена в ряд Фурье:
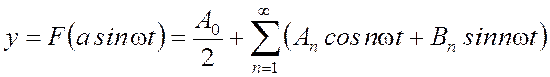. (3)
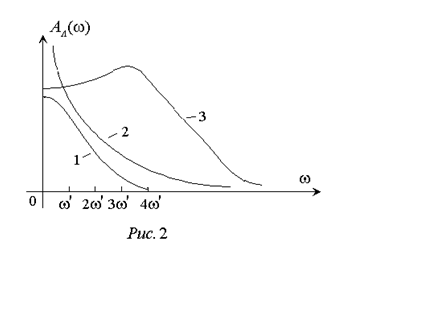
Этот сигнал преобразуется линейной частью в соответствии с ее динамическими характеристиками. Если степень многочлена R(s) в числителе передаточной функции линейной части меньше степени многочлена Q(s) в знаменателе, то на высоких частотах значения амплитудно-частотной характеристики линейной части
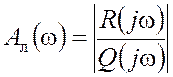
уменьшаются и
при 
стремятся к нулю (рис.2).
Скорость уменьшения Aл(w) с увеличением частоты определяет наличие у линейной части свойства фильтра:
Aл(nw)<<Aл(w), n=2,3,… (4)
При наличии такого свойства линейная часть (1) будет хорошо пропускать первую гармонику нелинейных колебаний (3) и ослаблять все высшие гармоники. Кроме того, в разложении Фурье, как правило, амплитуды гармоник с увеличением n также уменьшаются. Таким образом, ясно, что закон изменения сигнала x на входе нелинейного звена действительно окажется по форме близким к (2):
или 
, где
наличие постоянной составляющей x0 соответствует случаю несимметричных колебаний,
обусловленных либо несимметричными нелинейностями, либо приложением внешнего
воздействия. В этом случае задача расчета сводится к определению трех
параметров: a*, w*, x0, а в случае симметричных
колебаний – только a* и w*.
С учетом сказанного ясно, что для решения этой задачи в первом приближении достаточно исследовать прохождение по всей замкнутой цепи только первой гармоники сигнала y, то есть использовать следующее приближенное описание сигнала на выходе нелинейного звена:
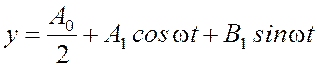. (5)
Такое приближение в большинстве случаев обеспечивает удовлетворительную точность анализа процессов в нелинейных системах. Границы его применимости определяются наличием свойства фильтра у линейной части при w=w*.
Соотношение (5) преобразуется следующим образом:
,
,
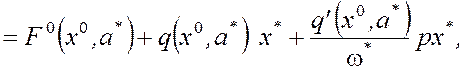
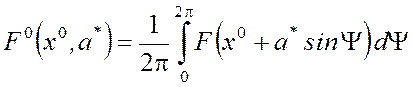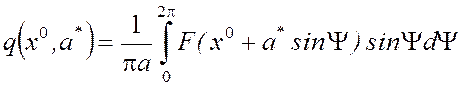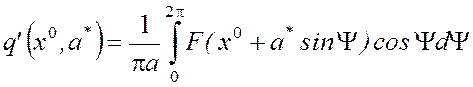, (6)
где F0(x0,a*) - постоянная составляющая сигнала на выходе нелинейного звена при несимметричных колебаниях, q(x0,a*) и q'(x0,a*) - коэффициенты гармонической линеаризации.
Проведем раздельное исследование симметричных и несимметричных автоколебаний.
А. Для случая симметричныхколебаний (x0=0, F0(x0,a*)=0) соотношения (6) упрощаются и вводится передаточная функция гармонически линеаризованного нелинейного звена:
,
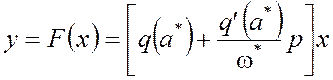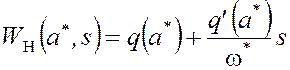. (7)
Из (7) видно, что параметры и характеристики линеаризованного звена, в отличие от линейных звеньев, зависят не только от частоты, но и от амплитуды колебаний на входе. Выражения для коэффициентов гармонической линеаризации типовых нелинейностей приводятся в литературе [1,2]. Применение гармонической линеаризации нелинейной части САУ позволяет использовать для ее анализа результаты теории линейных систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.