7. Запустить командой Start из меню Simulation моделирование системы. Зарегистрировать для отчета
график процесса x(t). В случае наблюдения установившегося колебательного
процесса измерить его период и амплитуду, а в случае несимметричных колебаний -
еще и постоянное смещение ![]() .
.
8. Повторить п. 7 для g0 = 80.
9. Установить значение коэффициента передачи линейной части k = 5 и повторить п. 7 для g0 = 80 и g0 = 10.
10. Обеспечить регистрацию с помощью блоков “Scope” графиков сигналов на выходе нелинейности и линейной части модели. Зарегистрировать указанные графики для последнего сочетания параметров k и g0.
11. По последнему из зарегистрированных графиков
автоколебательного процесса x(t) определить период T*автоколебаний
в системе и их круговую частоту 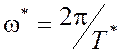 .
.
12. Выделить модель линейной части системы, исключив из используемой выше модели нелинейность и главную обратную связь.
13. Предусмотреть подачу на вход линейной части гармонического сигнала с помощью блока “SineWave” из раздела Sourses и регистрацию графика выходного сигнала y(t) с помощью блока “Scope”.
14. Подавая на вход линейной части гармонический сигнал с единичной амплитудой и частотой w*, 2w*, 3w*, зарегистрировать графики выходного сигнала линейной части и определить значения его амплитуды.
15. Повторить пункты 2-14 для второй модели нелинейной системы (с четным номером), используя значения k=1 и k=2, g0 = 10 и g0 = 30.
3. Содержание отчета
1. Структурные схемы исследуемых моделей.
2. Временные диаграммы процессов, зарегистрированных в ходе лабораторной работы, и измеренные значения параметров автоколебаний.
3. Расчет параметров автоколебаний для всех вариантов моделируемых систем методом гармонической линеаризации (в случае его неприменимости использовать метод припасовывания [1] ).
4. Результаты проверки наличия свойства фильтра для линейных частей исследованных моделей экспериментальным или расчетным путем.
Литература
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975.
2. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. М.: Наука, 1979.
3. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования: Учебное пособие. СПб.: БГТУ, 1994.
Цель работы - ознакомление с модификацией критерия абсолютной устойчивости В.М. Попова для нелинейных систем с неединственным состоянием равновесия.
1. Основные сведения из теории
Частотный критерий В.М. Попова сформулирован для нелинейных систем с устойчивой линейной частью и позволяет исследовать устойчивость нулевого равновесного состояния в целом, но не для одной фиксированной характеристики нелинейного элемента, а для некоторого семейства этих характеристик, принадлежащих к какому-либо классу [1,3]. Определенное таким образом состояние равновесия называют абсолютно устойчивым.
Наиболее часто для систем со
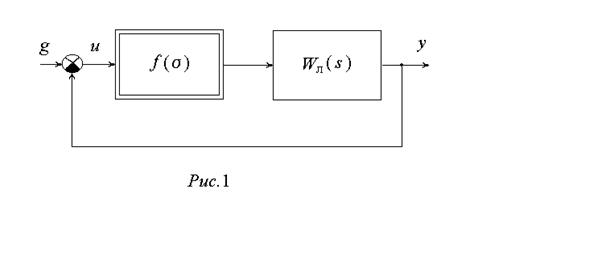
структурной схемой, приведенной на рис.1, рассматривают нелинейные
характеристики, заключенные в секторе [0,![]() ]. Обратимся к структуре системы с нелинейностью,
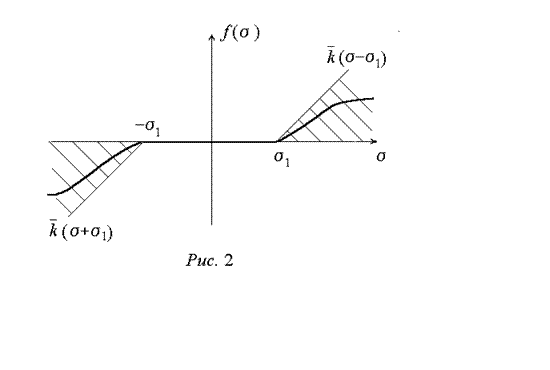
содержащей зону нечувствительности, и нейтрально устойчивой [4] линейной частью
с передаточной функцией
]. Обратимся к структуре системы с нелинейностью,
содержащей зону нечувствительности, и нейтрально устойчивой [4] линейной частью
с передаточной функцией ![]() (рис. 1, 2).
(рис. 1, 2).
 |
Пусть все полюсы ![]() лежат
слева, за исключением одного, равного
нулю, причем
лежат
слева, за исключением одного, равного
нулю, причем 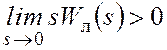 .
.
 |
![]()
а вне этого отрезка лежит внутри заштрихованных секторов, то есть
![]()
![]() (1)
(1)
причем выполнены условия:
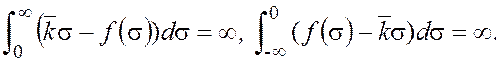 (2)
(2)
Тогда, если найдется
вещественное неотрицательное число ![]() такое, что
такое, что ![]() не является
полюсом
не является
полюсом ![]() , и при всех
, и при всех ![]() выполнено
частотное неравенство
выполнено
частотное неравенство
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.