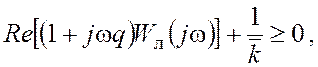Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 13

                                   (3)   

то  при любых ограниченных начальных условиях процесс  остается огра-ниченным при  , а  при    стремится к одной из точек отрезка покоя . В этом случае говорят, что отрезок покоя точечно устойчив в целом.

Частотное неравенство (3) совпадает с достаточным условием устойчивости, составляющим суть критерия В.М. Попова, и имеет ту же геометрическую интерпретацию с точностью до того, что допускается проведение прямой, проходящей через точку  и касающейся годографа модифицированной частотной характеристики [3,4].

Как видно из приведенной формулировки, наклон прямой не должен быть отрицательным. Кроме того, условия (1) не допускают, чтобы  касалась оси абсцисс вне отрезка покоя, а  условия (2) равносильны требованию «неплотного прилегания»  к лучам.

Для того чтобы проверить выполнение критерия Гелига, следует построить годограф модифицированной частотной характеристики линейной части

где  

, и попытаться провести прямую, имеющую неотрицательный коэффициент наклона  проходящую через точку  и оставляющую годограф   справа [4]. Если это удается, то отрезок покоя точечно устойчив в целом.

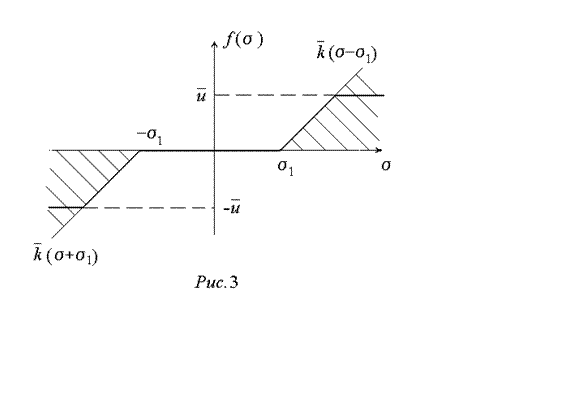
В лабораторной работе исследуется поведение следящей системы, в которой датчик рассогласования имеет зону нечувствительности, а усилитель -ограниченную зону линейности, то есть насыщение. Эти две нелинейности можно описать одной нелинейной зависимостью (рис.3). При  и  приходим к линейной модели, если остальные элементы  следящей системы описываются линейным соотношениями.

Передаточную функцию скорректированной линейной части примем в виде

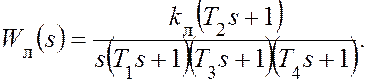                                                  (4)                                                 

Из линейной теории следует, что пи соответствующем выборе параметров из условия

можно обеспечить заданные динамические свойства замкнутой линейной системы.

Для нелинейной модели следящей системы достаточное условие устойчивости (3) можно записать в виде

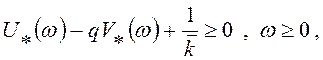
или для случая ПФ линейной части  (4) – в форме неравенства

                                                       (5)                                 

где ,  - соответственно вещественная и мнимая части функции  , причем

,

,

.

Условию (5) можно дать специальную геометрическую интерпретацию. Если ввести условную частотную характеристику  и построить ее годограф, то условие устойчивости (5) означает возможность провести прямую с неположительным коэффициентом наклона  через точку так, чтобы годограф не заходил левее ее. По виду годографа  можно определить предельное значение коэффициента передачи линейной части , превышение которого приводит к нарушению точечной устойчивости в целом рассматриваемого отрезка.

2. Описание  модели нелинейной системы

Модель  нелинейной системы строится в пакете SIMULINK в соответствии со схемой, представленной на рис. 4.

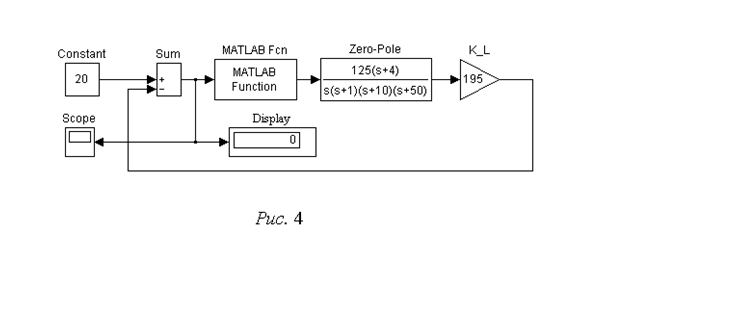Модель линейной части системы, задаваемой ПФ вида (4), набирается с помощью блока “Zero-Pole”, описывающего нормированную ПФ:

в zpk-форме, и блока “Gain”, задающего варьируемый коэффициент передачи k_л, обозначенный на схеме  K_L. Постоянные  времени  линейной части  приняты  здесь следующими: T₁ =1c, T₂ = 0,25 c, T₃ = 0,1 c, T₄ =0,02 c.

Нелинейность, представленная на рис. 3,  реализуется с помощью блока “MATLAB Fcn”, извлекаемого из раздела Functions & Tables библиотеки. Этот блок позволяет применить к входному сигналу процедуру обработки, реализованную в виде М-файла.

Последовательно соединенные нелинейности типа зоны нечувстви-тельности и насыщения с заданной крутизной линейного участка  могут быть описаны c помощью функции nonlin:

function y = nonlin (x, k_, sig1 , u_ )

             sig2 = sig1 + u_/k;

       if abs(x) <= sig1

             y = 0;                                                                                          

       elseif abs(x) < sig2

             y = k_*(x – sign(x)*sig1);

       else