Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 6

4. Установить значения g₀ = 30, f₀ = 10. Зарегистрировать для отчета график x(t), измерить величину x_уст и заполнить строку 20 табл. 2.

3. Содержание отчета

1.  Структурные схемы системы, соответствующие выполненным разделам.

2.  Результаты выполнения п.6 раздела А.

3.  Заполненная таблица результатов, содержащая все строки табл. 2, соответствующие выполненным разделам, и кривые соответствующих переходных процессов.

4.  Результаты расчета критических значений коэффициента усиления разомкнутой системы для всех выполненных разделов.

5. Выводы по каждому выполненному разделу работы.

Литература

1.  Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975.

2.  Андриевский Б.Р., Фрадков А.Л. Элементы математического моделирования в программных средах MATLAB 5 и Scilab. СПб.: Наука, 2001.

3.  Гультяев А. Визуальное моделирование в среде MATLAB: Учебный курс. СПб.: Питер, 2000.

Лабораторная работа № 2

ИССЛЕДОВАНИЕ САУ С ДИСКРЕТНОЙ КОРРЕКЦИЕЙ

Цель работы - ознакомление с методикой синтеза алгоритмов управления, реализуемых БЦВМ, и исследование процессов в дискретных системах.

1.  Основные сведения из теории

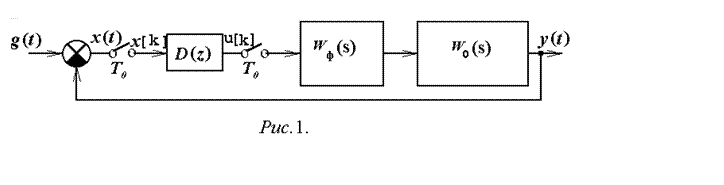
Упрощенная структурная схема системы управления с БЦВМ изображена на рис.1, где  - передаточная функция (ПФ) непрерывной части, 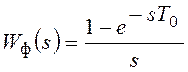 - ПФ формирующего устройства (экстраполятора нулевого порядка),  - ПФ дискретного фильтра, отражающего алгоритм управления, реализуемый БЦВМ.

Ключи, периодически замыкающиеся с периодом , отражают эффект квантования по времени в преобразователях аналоговой величины в код и кода в аналоговую величину.

При таком подходе, не учитывающем эффекта квантования по уровню, структурная схема цифровой САУ соответствует импульсной системе с дискретной коррекцией.

Обычно при проектировании цифровых систем значение периода дискретности  T₀ выбирается максимально допустимым. При этом удается снизить требования, предъявляемые к цифровой машине в отношении быстродействия, но зато специфические свойства систем, связанные с квантованием сигналов по времени, проявляются особенно сильно.

Исследование динамических свойств непрерывно-дискретных систем существенно упрощается, если рассматривать поведение системы только в дискретные моменты времени kT₀ , k=1,2,… . В этом случае динамика сиcтемы описывается разностными уравнениями или дискретными передаточными функциями.

Применительно к структуре САУ, показанной на рис.1, дискретная ПФ разомкнутой системы равна [1]:

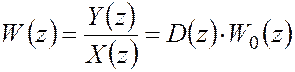,                                       (1)   где дискретная ПФ приведенной непрерывной части W₀(z) определяется или путем z-преобразования переходной функции непрерывной части согласно выражению

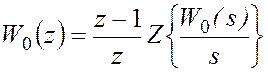                      ,                                       (2)

или вычислением матриц P, Q  эквивалентной дискретной модели как подматриц “расширенной” матричной экспоненты, формируемой по уравнениям состояния непрерывной части системы [2]. В последнем случае дискретная ПФ определяется  известной формулой:

                     .                                      (3)

Такой метод вычислений реализован в известной программе c2d ППП Control System Toolbox, входящего в среду MATLAB, и может быть рекомендован для построения дискретных моделей при известном периоде дискретности T₀ (на заключительном этапе анализа).

Линейные дискретные алгоритмы управления могут быть описаны раз-ностным  уравнением вида

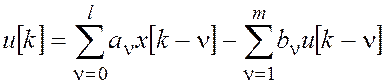                                         ,                                             (4)                                                                             

где - число запоминаемых значений величины, поступающей на вход дискретного корректирующего устройства (цифровой машины),  – число запоминаемых значений управляющего сигнала, a_v и b_v - постоянные коэффициенты (параметры закона управления).

Воспользовавшись аппаратом z-преобразования, от уравнения (4) можно перейти к ПФ дискретного корректирующего устройства: