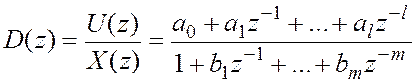 .
.
При синтезе дискретных
алгоритмов управления используются логарифмические псевдочастотные
характеристики (ЛПЧХ). Для перехода к псевдочастоте применяется так называемое ![]() - преобразование, то есть используется подстановка [1]:
- преобразование, то есть используется подстановка [1]:
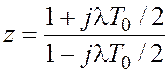 . (5)
. (5)
где ![]() - абсолютная псевдочастота.
- абсолютная псевдочастота.
Тогда псевдочастотная ПФ разомкнутой системы примет вид
![]() .
(6)
.
(6)
Расчёт дискретных систем
вызывает большие трудности в связи с более сложной процедурой получения
частотных характеристик, в частности, ![]() . В
работе используется приближённый способ построения ЛПЧХ, основанный на
раздельном их построении для области низких и высоких частот [1]. В частном
случае, когда период дискретности
. В
работе используется приближённый способ построения ЛПЧХ, основанный на
раздельном их построении для области низких и высоких частот [1]. В частном
случае, когда период дискретности ![]() выбран так, что для любой
постоянной времени
выбран так, что для любой
постоянной времени ![]() , входящей в ПФ объекта
, входящей в ПФ объекта ![]() , выполняется условие
, выполняется условие ![]() , частотная ПФ
, частотная ПФ ![]() ,
входящая в выражение (6), может быть определена без предварительного
вычисления
,
входящая в выражение (6), может быть определена без предварительного
вычисления ![]() следующим образом:
следующим образом:
![]() .
(7)
.
(7)
В лабораторной работе производится выбор алгоритма БЦВМ для канала угловой стабилизации ракеты, причём исследование ведётся по максимально упрощённым динамическим схемам, учитывающим только основное движение ракеты как жёсткого тела. Рассматриваются следующие формы упрощенной ПФ ЛА:
- форма 1
![]() (8)
(8)
- форма 2
![]() (9)
(9)
Выполнив z-преобразование по формуле (2) для объекта с ПФ (8) и последующей заменой (5), приходим к частотной ПФ неизменяемой части:
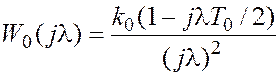 .
(10)
.
(10)
Для определения частотной ПФ,
соответствующей объекту с ПФ (9), следует поступить аналогично. Тогда с учетом
условия ![]() для области низких частот получим
для области низких частот получим
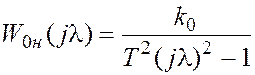 .
(11)
.
(11)
В области высоких частот псевдочастотная характеристика (ПЧХ) объекта (9) приводится к виду (10), где параметр k0 следует заменить на k0/T2 . На основании формул (11) и (10) приближенное представление ПЧХ для всего частотного диапазона определится выражением
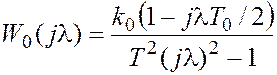 .
(12)
.
(12)
Таким образом, и в этом случае приходим к приближенному выражению (7).
Нетрудно убедиться, что при отсутствии
дискретной коррекции, то есть при ![]() , замкнутая система как
с объектом (8), так и с объектом (9) не может быть устойчивой. Для обеспечения
устойчивости дискретный фильтр должен создавать опережение по фазе.
Следовательно, ПЧХ этого фильтра можно выбрать в виде
, замкнутая система как
с объектом (8), так и с объектом (9) не может быть устойчивой. Для обеспечения
устойчивости дискретный фильтр должен создавать опережение по фазе.
Следовательно, ПЧХ этого фильтра можно выбрать в виде
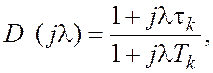
![]() . (13)
. (13)
Из (10) и (12) с учётом (13) следуют желаемые ПЧХ разомкнутой системы для рассматриваемых моделей объектов:
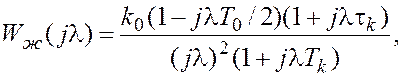 (14)
(14)
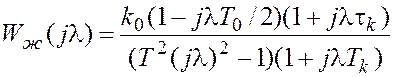 .
(15)
.
(15)
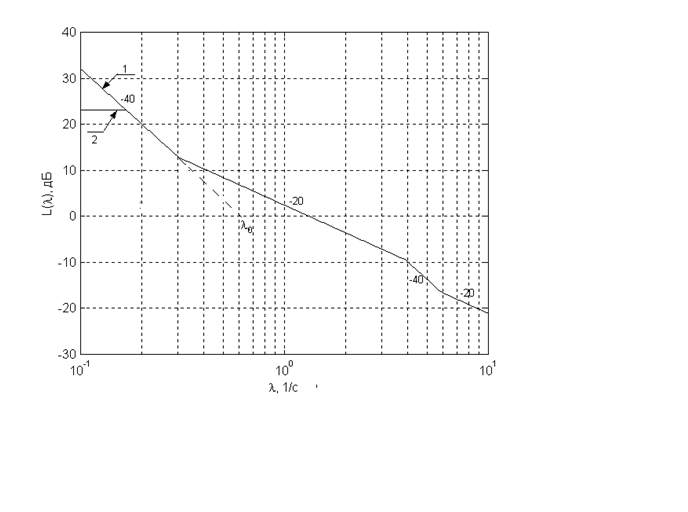 |
Рис. 2
Базовая частота для первой из них
![]() ,
(16)
,
(16)
а для второй
![]() .
(17)
.
(17)
Так как в низкочастотной области логарифмические характеристики непрерывной и дискретной систем практически совпадают, для их формирования в этой области можно применять все существующие рекомендации, разработанные для синтеза непрерывных систем [3].
В замкнутой дискретной системе, ПЧХ которой в разомкнутом состоянии приближенно приводится к виду
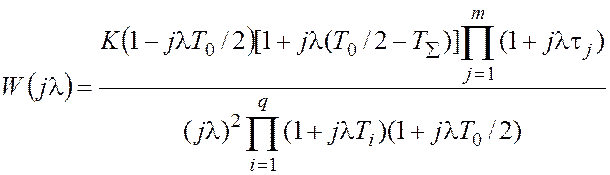 , где
, где 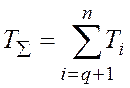 - сумма малых
постоянных времени, а постоянным времени
- сумма малых
постоянных времени, а постоянным времени ![]() соответствуют
сопрягающие частоты, меньшие частоты среза, будет обеспечен заданный показатель
колебательности М, если выполняются следующие
условия [1]:
соответствуют
сопрягающие частоты, меньшие частоты среза, будет обеспечен заданный показатель
колебательности М, если выполняются следующие
условия [1]:
- сумма сопрягающих частот,
меньших частоты среза ![]() , должна удовлетворять условию
, должна удовлетворять условию
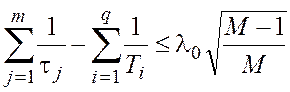 ,
,
- сумма малых постоянных
времени, соответствующих сопрягающим частотам, большим частоты среза ![]() , должна быть ограничена, а именно
, должна быть ограничена, а именно
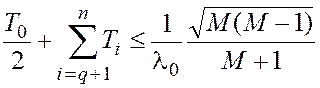 .
.
Применительно к системе с
дискретной коррекцией, синтезируемой в данной работе с ПЧХ вида (14), (15),
параметры ![]() ,
, ![]() и
период дискретности
и
период дискретности ![]() должны удовлетворять условиям
должны удовлетворять условиям
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.