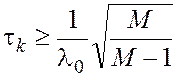 ,
(18)
,
(18)
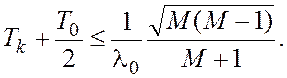 (19)
(19)
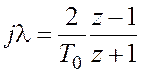
и приводится к виду
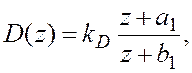 (20)
(20)
где
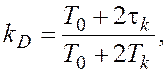
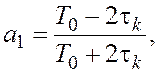
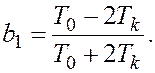
2. Порядок выполнения работы
Исследование проводится методом моделирования на ПЭВМ IBM PC в среде MATLAB 5.*/SIMULINK [4].
1. Для заданного преподавателем
варианта исходных данных, представ-ленных для объекта типа (8) в табл. 1, а
для объекта типа (9) - в табл. 2, выбрать исходные значения параметров объекта ![]() (или
(или ![]() и
и ![]() ) и требуемое значение показателя
колебательности М.
) и требуемое значение показателя
колебательности М.
Таблица 1
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
|
|
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
|
|
1.3 1.6 |
1.4 1.7 |
1.3 1.7 |
1.4 1.7 |
1.5 1.9 |
Таблица 2
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
|
|
4.0 |
4.0 |
5.0 |
4.5 |
5.0 |
|
|
2.0 |
1.5 |
2.0 |
2.0 |
2.0 |
|
|
1.5 |
1.5 |
1.4 |
1.4 |
1.5 |
2. По формулам (16)-(19)
рассчитать ![]() и требуемые для обеспечения заданного
запаса устойчивости значения постоянных времени
и требуемые для обеспечения заданного
запаса устойчивости значения постоянных времени ![]() ,
, ![]() и период дискретности
и период дискретности ![]() , положив
, положив 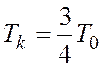 .
Вычислить коэффициенты
.
Вычислить коэффициенты ![]() передаточной функции (20)
дискретного фильтра.
передаточной функции (20)
дискретного фильтра.
3. Войти в среду MATLAB и запустить SIMULINK, открыв пустое окно для создания S-модели дискретного регулятора. Извлечь из раздела библиотеки Control SystemToolbox блок “LTI System” ( lti-блок). Открыв диалоговую панель для настройки параметров, в окне LTI system variable набрать команду zpk (-a1, -b1, kD, T0) в соответствии с расчётными значениями, полученными в п. 2. Тем самым будет сформирована lti-модель дискретного регулятора в zpk-форме.
Получить и зафиксировать для
отчёта переходную характеристику дискретного корректирующего устройства (20) на
интервале ![]() [0, 2].
[0, 2].
4. Набрать модель замкнутой дискретной системы в соответствии со структурной схемой (рис.1) и расчетными параметрами, причем построенный в п. 3 дискретный lti-блок регулятора может быть включен в ее состав, а экстраполятор нулевого порядка извлечен в виде блока “Zero-OrderHold” из раздела библиотеки Discrete .
Построить и зафиксировать
переходную характеристику замкнутой дискретной системы. Моделирование
выполнить на интервале ![]() [0, 4].
[0, 4].
5. Произвести моделирование
дискретной системы при отсутствии дис-кретной коррекции, то есть при ![]() или
или ![]()
![]()
![]() , на интер-вале
, на интер-вале ![]() [0, 10].
[0, 10].
3. Содержание отчета
1. Структурная схема цифровой системы.
2. Результаты расчета параметров дискретного корректирующего устройства .
3. Переходные характеристики по п. 2.3-2.5.
4. ЛПЧХ разомкнутой системы без коррекции и с коррекцией при заданных параметрах объекта и расчетных параметрах дискретного корректирующего устройства. Результаты исследования устойчивости и оценка показателя колебательности.
Литература
1. Динамика систем управления ракет с бортовыми цифровыми вычислительными машинами/ Под ред. М. С. Хитрика и С. М. Федорова. М.: Машиностроение, 1976.
2. Андриевский Б.Р. Анализ систем в пространстве состояний. СПб.: ИПМаш РАН, 1997.
3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975.
4. Андриевский Б.Р., Фрадков А.Л. Элементы математического моделирования в программных средах MATLAB 5 и Scilab. СПб.: Наука, 2001.
Лабораторная работа № 3
ИССЛЕДОВАНИЕ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНОЙ СИСТЕМЕ
Цели работы - изучение особенностей преобразования сигнала и закономерностей возникновения автоколебаний в нелинейных САУ, знакомство с методом гармонической линеаризации и проверка условий его применимости.
1. Основные сведения из теории
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.