Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 11

Б. Перейдем к исследованию несимметричных колебаний, которые при симметричной нелинейности могут иметь место в статической системе при наличии постоянного внешнего воздействия.

Пусть задана нелинейная САУ, динамика которой относительно входа   нелинейности описывается уравнением

.                                 (13)

Если считать внешнее воздействие постоянным (), то для статических систем, у которых , уравнение (13) упростится:

                              (14)

Как отмечалось выше, решение уравнения (14) ищется в форме

, причем являются искомыми параметрами автоколебаний. С учетом со-отношений (6) уравнение (14) примет вид

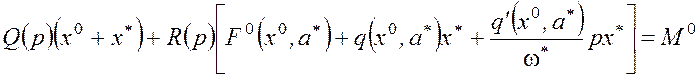.  (15)

Уравнение (15) разбивается на два следующих:

                                                   (16)

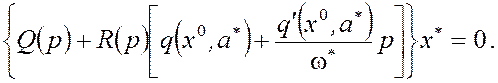                             (17)

Параметры  гармонических колебаний находятся из характеристического уравнения, соответствующего уравнению (17):

или из эквивалентной системы нелинейных алгебраических уравнений:

                             (18)

Совместное решение системы уравнений (18) и уравнения (16) позволит найти искомые параметры автоколебаний  при заданных параметрах системы.       

Дополнения.

1. Решение систем нелинейных алгебраических уравнений (9) для случая А и (16), (18) для случая Б целесообразно производить в среде MATLAB с помощью функции fsolve [3] (cтр. 152).

2. Постоянная составляющая и коэффициенты гармонической линеариза-ции  нелинейностей при несимметричных колебаниях определяются следую-щим образом [2]:

-для нелинейности типа “насыщение” (рис. 3)

 ,

;

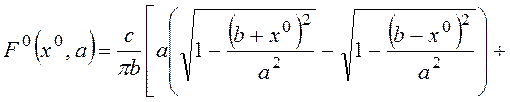
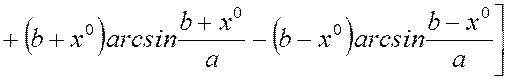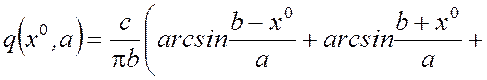
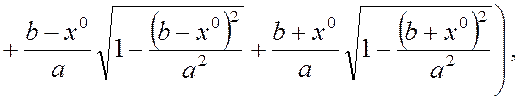
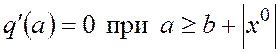-для двухпозиционного реле с положительным гистерезисом (рис. 5)

.

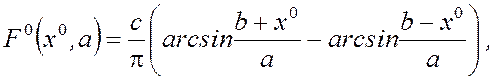
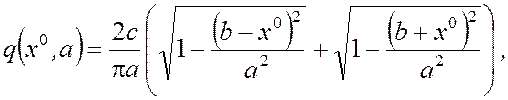
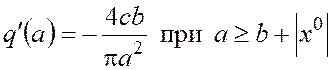2. Порядок  выполнения   работы

Задание по лабораторной работе предусматривает исследование двух моделей замкнутой нелинейной системы, задаваемых преподавателем в соответствии с табл. 1 (структура и параметры первой модели выбираются с нечетным, второй – с четным номером).

Исследование производится путем моделирования в среде MATLAB 5.*/SIMULINK.

1. Запустить SIMULINK из MATLAB 5.0 и построить первую модель (с нечетным номером).

2. Установить значения параметров звеньев модели в соответствии с заданным вариантом.

3. Установить значение коэффициента передачи линейной части k = 1.

4. С помощью блока-константы “Constant” из раздела Sourses установить значения g₀ = 10.

Таблица 1

Варианты заданий

№ варианта	Нелинейная часть	Линейная часть
1	b = 20 c = 40	T = 0.2
2	b = 20 c = 20	T1= 0,05; T2= 1
3	b = 20 c = 20	T = 2
4	b = 20 c = 20	T1= 1; T2= 0,5
5	b = 20 c = 20	T1= 2; T2= 1
6	b = 20 c = 20	T = 0,1

5. Обеспечить регистрацию графика сигнала ошибки x(t) путем подачи этого сигнала на вход блока “Scope”. Указанное устройство извлекается из раздела Sinks библиотеки.

6. Войти в меню Simulation, открыть диалоговое окно Parameters и в поле Stoptime установить время остановки равным 30 с.