Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 15

1. Первозванский А.А. Курс теории автоматического управления. М.: Наука, 1986.

2. Методы исследования нелинейных систем автоматического управления /Под ред. Р.А.Нелепина. М.: Наука, 1975.

3. Справочник по теории автоматического управления /Под ред. А.А.Кра-совского.  M.: Наука, 1987.

4. Бесекерский В.А., Попов Е.П. Теория систем автоматического регули-рования. M.: Наука, 1975.

Лабораторная работа  № 5

ИССЛЕДОВАНИЕ СИСТЕМЫ С ПЕРЕМЕННОЙ СТРУКТУРОЙ

Цель работы - исследование реальных скользящих режимов в системах с переменной структурой методом фазовой плоскости.

1. Основные сведения  из теории

Системы с переменной структурой (СПС) – это специальный класс нелинейных систем, в которых происходит переключение регуляторов (или их параметров) по сигналам блока изменения структуры (БИС) в зависимости от значений переменных состояния объекта [1].

Обычно каждый из регуляторов (образующий вместе с объектом соответствующую «структуру») является линейным, но благодаря переключению структур закон управления получается существенно нелинейным. Как правило, СПС состоит из двух линейных регуляторов и блока изменения структуры, работающего по релейному закону. Структурная схема такой системы приведена на  рис. 1, где P₁, P₂ - линейные регуляторы; g(t) - задающее воздействие; y(t) - выход объекта; u(t)- управляющее воздействие;  БИС - блок изменения структуры; ОУ - объект управления; ИУ - исполнительное устройство.

Переключение структур в СПС осуществляется для повышения качества процессов управления и упрощения синтеза регулятора.

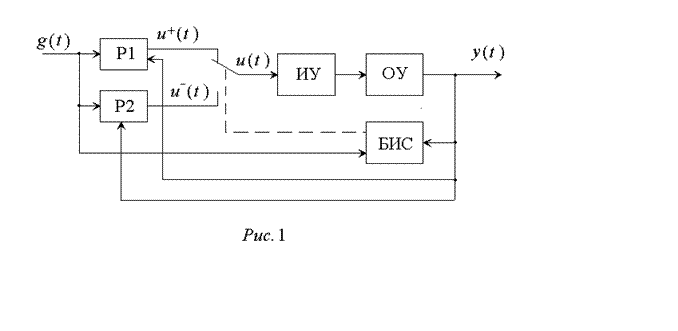В качестве примера СПС можно рассмотреть систему, у которой каждая из линейных структур является гармоническим осциллятором (консервативным звеном), но с разными параметрами собственных колебаний, а благодаря переключению структуры получается устойчивая система с малым временем переходного процесса.

На рис. 2, а, б показаны фазовые траектории и переходные процессы в составных линейных системах, а на рис. 2, в – фазовые траектории и переход-ный процесс в СПС [1].

Линиями переключения в данном примере являются оси координат. Уравнения линий переключения: x= 0 и .

Другой пример СПС – система с переменным демпфированием [1], в которой коэффициент обратной связи по производной в законе управления переключается в зависимости от рассогласования. В результате удается добиться малого времени переходного процесса при незначительном перерегулировании.

Рассмотрим работу СПС более подробно. Пусть в фазовом пространстве (пространстве состояний) системы имеется некоторая поверхность (поверхность переключения), заданная уравнением S(X) = 0, где X=X(t) - вектор состояния системы. Эта поверхность делит пространство состояний на области, где  и . Так как при переключении u(t) обычно меняется скачком, поверхность S(X) называется также поверхностью разрыва [2]. При переходе изображающей точки через поверхность S(X) возможны следующие случаи: 1) вектор фазовой скорости направлен в область, смежную с исходной (рис. 3, а); 2) вектор фазовой скорости направлен вдоль поверхности разрыва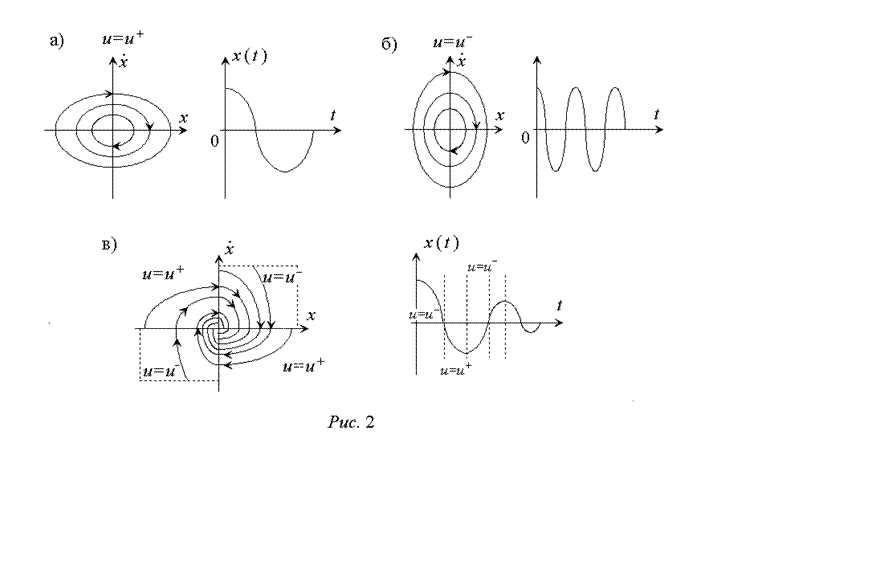
(рис. 3, б); 3) вектор фазовой скорости после переключения направлен в исходную область (рис. 3, в).

Случай 1 имеет место в рассмотренных выше примерах СПС. В случае 2 фазовая траектория, соответствующая управлению , лежит на поверхности S(X)=0. Это явление характерно для оптимальных по быстродействию систем управления [3,4], однако оно практически недостижимо из-за погрешностей в реализации. Случай 3 отличается от 1 и 2  тем, что здесь в процессе движения моменты переключения не изолированы друг от друга. Теоретически переключение структур наступает в сколь угодно близкие между собой моменты времени. Изображающая точка, попав на поверхность разрыва, должна на ней остаться, так как вектор фазовой скорости всегда направлен в сторону этой поверхности. Такой вид движения системы называется идеальным  скользящим режимом [1, 2, 5].