Теория управления: Лабораторный практикум (Лабораторные работы № 1-5: Исследование основных методов повышения точности систем автоматического управления. Исследование системы с переменной структурой), страница 2

Поэтому возможность повышения точности исследуемой САУ лишь за счет увеличения коэффициента усиления разомкнутой системы ограничена, причем максимально допустимое значение K₀ должно быть меньше K_0кр в соответствии с требуемым запасом устойчивости системы.

1.3. Введение производной

Введение производной от ошибки в закон регулирования может быть осуществлено за счет использования прямой параллельной корректирующей цепи с коэффициентом передачи k_п.

Передаточная функция разомкнутой скорректированной системы в этом случае имеет вид

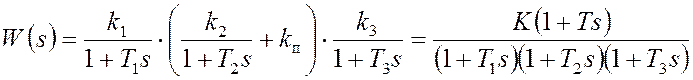, гдеK=k₁(k₂+k_п)k₃ - общий коэффициент усиления;  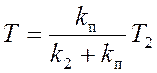- постоянная времени, определяющая уровень сигнала управления по производной.

Используя соотношение (2) или структурный признак астатизма [1], нетрудно убедиться, что система осталась статической как по задающему, так и по возмущающему воздействиям.

Характеристический полином замкнутой скорректированной системы имеет вид

.

Отсюда получаем условие для определения критического значения коэффициента усиления:

,

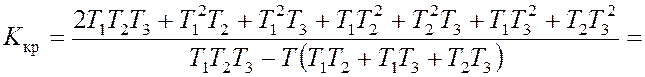
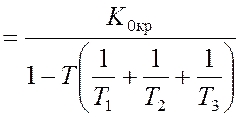.                                          (5)

Из формулы (5) видно, что, вводя производную в закон регулирования, можно значительно расширить границу увеличения коэффициента усиления и, следовательно, уменьшить обе составляющие ошибки.

1.4. Введение гибкой обратной связи

При добавлении в цепь единичной обратной связи системы дополнительного дифференцирующего звена с коэффициентом k'_ос (см. рис.1) передаточная функция обратной связи примет вид

.

В этом случае соответствующие передаточные функции замкнутой системы определяются по соотношениям

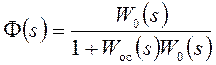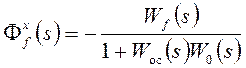, , .  (6)

На основе (6) получим характеристический полином замкнутой системы:

.

K_0кр определяется аналогично предыдущему подразделу.

1.5. Повышение порядка астатизма

При введении дополнительного идеального интегрирующего звена (см. рис.1) повышается порядок астатизма системы. Передаточная функция разомкнутой системы принимает вид

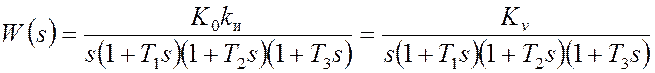,       (7)

где K_v = K₀k_и – новый коэффициент усиления разомкнутой системы, в рассматриваемом случае называемый добротностью по скорости [1] и приобретающий размерность с^-1. Ошибка системы в установившемся режиме работы может быть определена на основе (2):

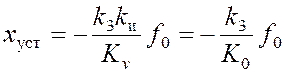.                                    (8)

Из формулы (8) следует, что скорректированная САУ стала астатической по задающему воздействию и осталась статической по отношению к возмущающему воздействию. Кроме того, из этой формулы следует, что при введении интеграла составляющая ошибки x_fможет возрасти, так как при введении интеграла обычно уменьшается запас устойчивости системы, что приводит к необходимости снижения коэффициента усиления.

На основе критерия Гурвица с учетом повышения степени характеристического полинома можно найти условие устойчивости для данной структурной схемы САУ:

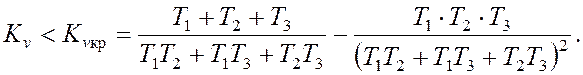              (9)

Нетрудно убедиться, что здесь критическое значение коэффициента усиления значительно меньше, чем при отсутствии интегрирующего звена.

Более эффективным является включение интегрирующего звена в состав регулятора (интегральный закон регулирования). Если в отличие от рис. 1 переместить интегратор до точки приложения возмущающего воздействия, передаточная функция (7) и условие (9) сохранятся, но на основе (2) можно убедиться в достижении теперь астатизма как по задающему, так и по возмущающему воздействиям. При воздействиях рассматриваемого вида необходимость снижения коэффициента усиления не повлияет на точность системы в установившемся режиме.

1.6. Повышение порядка астатизма введением изодромного звена

Повысить порядок астатизма системы можно также путем введения в прямую цепь изодромного звена (пропорционально-интегрального регулятора) с передаточной функцией (см. рис.1)

.

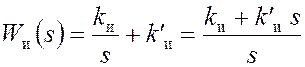Передаточная функция разомкнутой системы принимает вид

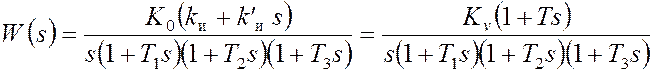, где K_v = K₀k_и – новый коэффициент усиления разомкнутой системы (добротность);  - новая постоянная времени.

Получить условие устойчивости для данной структуры  САУ и убедиться, что значение критического коэффициента усиления здесь выше, чем при введении в систему идеального интегратора, предлагается самостоятельно. Здесь может быть полезно также использование частотного критерия устойчивости Найквиста.