Цель лабораторной работы:
Исследовать систему стабилизации углового движения ЛА описываемую линейными дифференциальными уравнениями. Построить единичную переходную функцию, весовую функцию, АФЧХ разомкнутой системы, определить ограничение запаса устойчивости по фазе и амплитуде, построить АФЧХ замкнутой системы, определить положение полюсов и нулей.
Постановка задачи
Рассмотрим систему стабилизации углового движения ЛА относительно центра масс в продольной плоскости. В качестве программного движения принимается полёт ЛА на заданной высоте с постоянной скоростью. Динамика системы стабилизации описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения:
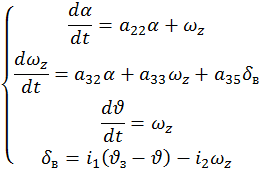
Где ![]() -
угол атаки,
-
угол атаки,![]() -
угол тангажа,
-
угол тангажа, ![]() -
угловая скорость тангажа,
-
угловая скорость тангажа, ![]() -
угол отклонения руля высоты,
-
угол отклонения руля высоты, ![]() -
известные динамические коэффициенты,
-
известные динамические коэффициенты, ![]() ,
, ![]() -
передаточные числа.
-
передаточные числа.
|
|||||||||||||||||||
 |
|||||||||||||||||||
|
|
||||||||||||||||||
|
|||||||||||||||||||
|
|
||||||||||||||||||
 |
 |
||||||||||||||||||



![]()
![]() - -
- -
|
|||||||

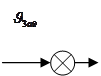
Рис.1
![]()
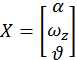
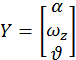
![]()
Составление
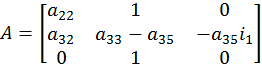
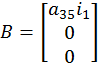
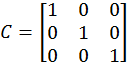
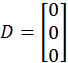
Исходные данные:
|
Вар. |
|
|
|
|
|
|
Кс |
Тс |
|
T1с |
|
3 |
-1,13 |
-3,14 |
-1,28 |
3,20 |
4,0 |
0,3 |
0.7884 |
0.4669 |
0.5627 |
0.8850 |
Листинг программы:
a22=-1.35;
a32=-1.2;
a33=-1.5;
a35=4;
i1=1;
i2=0.8;
A=[a22,1,0;a32,a33-a35*i2,-a35*i1;0,1,0];
B=[a35*i1;0;0];
C=[1,0,0;0,1,0;0,0,1];
D=[0;0;0];
L=ss(A,B,C,D);
step(L)
hF2 = figure;
impulse(L)
hF3 = figure;
bode(L)
hF4 = figure;
pzmap(L)
A1=[a22,1,0;a32,a33,0;0,1,0];
B1=[0;a35*i1;0];
C1=[0,i2,i1];
D1=[0];
L1=ss(A1,B1,C1,D1);
hF5 = figure;
bode(L1)
Графики:
1)Единичная
переходная функция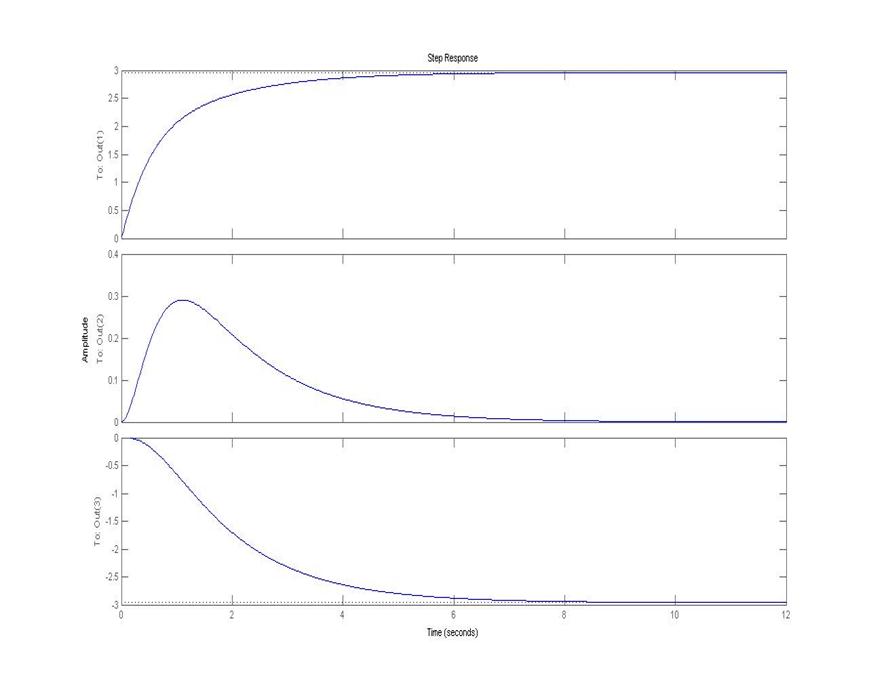
2)Весовая функция
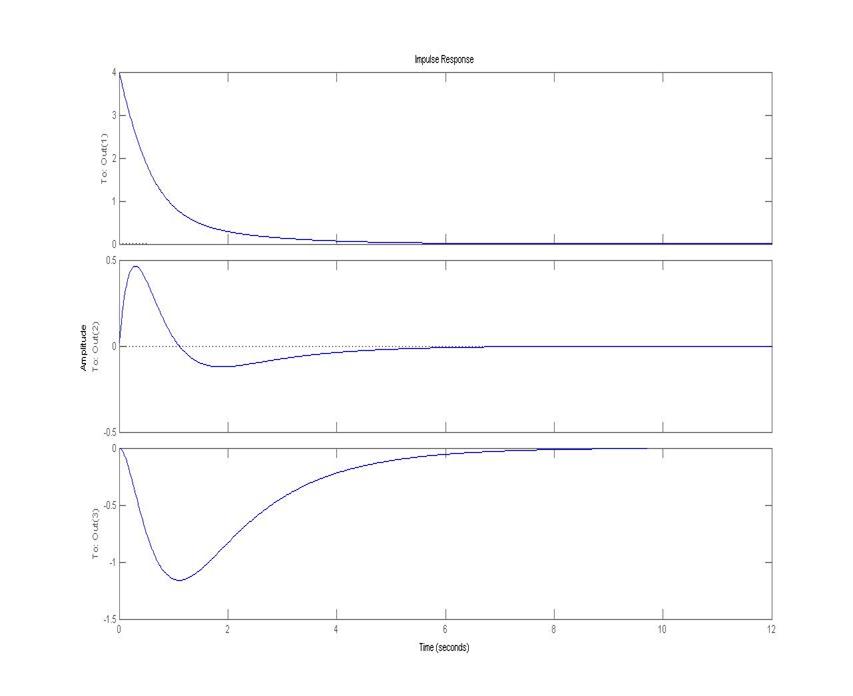
3)АФЧХ замкнутой системы
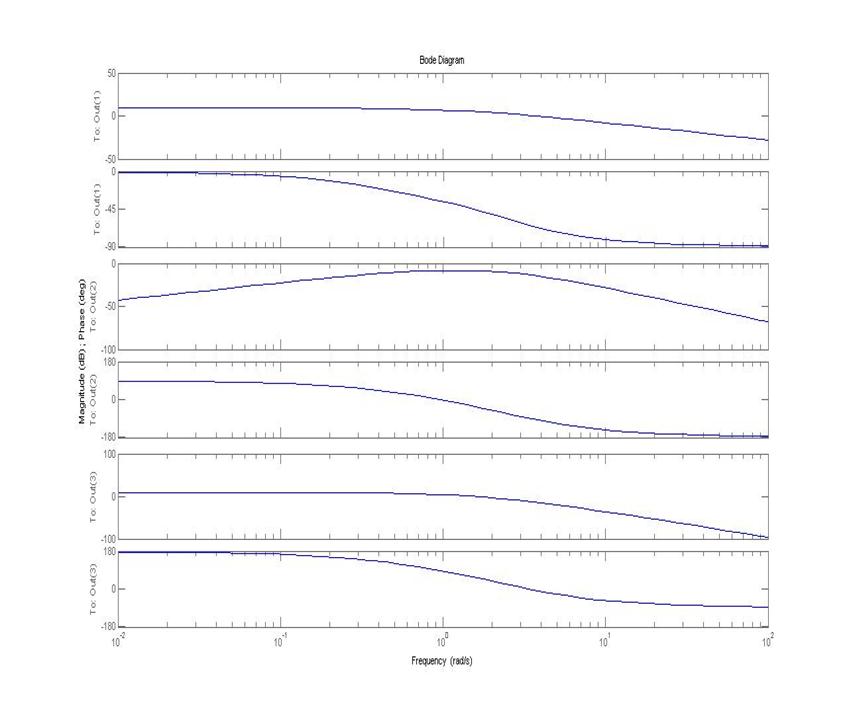
4)АФЧХ разомкнутой системы
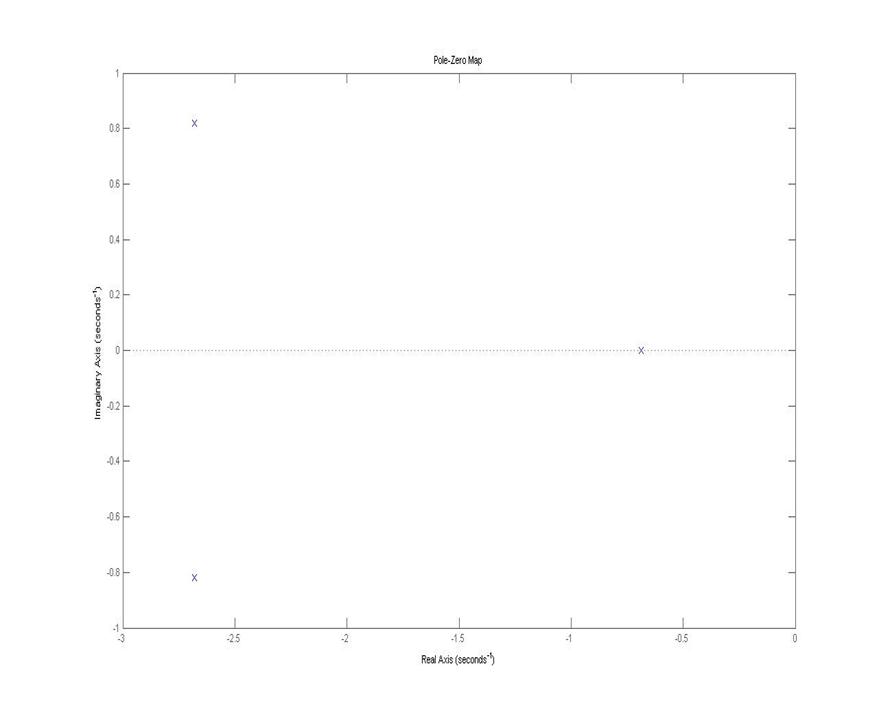
5)Полюса и нули
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.