Балтийский государственный
технический университет
им. Д. Ф. Устинова
«ВОЕНМЕХ»
Кафедра А5
Лабораторная работа по ТАУ №5
«Исследование переходных процессов и качество регулирования САУ»
Вариант №18
|
Санкт-Петербург 2012 год
Содержание лабораторной работы.
Цель лабораторной работы………………………………………………….стр. 3
Описание лабораторной работы……………………………………………стр. 3
Исходные данные к лабораторной работе…………………………………стр. 4
Листинг программы ………………………………………………………...стр. 6
Выводы ………………………………………………………………………стр. 7
Цель работы: построение переходных процессов аналитическими методами и моделированием, установление связи между видом логарифмических частотных характеристик и характером переходных процессов.
Описание лабораторной работы.
Рассмотрим систему стабилизации угла крена ЛА, которая задается следующей системой уравнений:
|
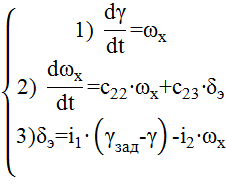
В данной системе уравнений (1) введены следующие обозначения: γ – угол крена, δэ – угол отклонения рулей элеронов, ωх – угловая скорость крена, сij – известные динамические коэффициенты, i1, i2 – передаточные числа, γзад – известная функция, задающая программу угла крена. Уравнения 1)-2) описывают динамику ЛА, уравнение 3) – уравнение системы управления. При этом рулевая машинка считается безынерционной.
Системе уравнений (1) соответствует структурная схема системы стабилизации угла рыскания, приведенная на рис. 1.
|
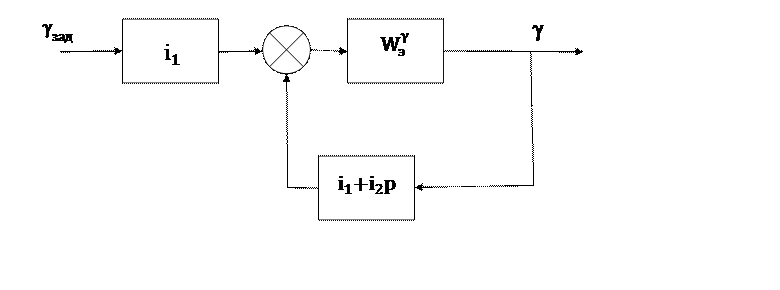
Исходные данные к лабораторной работе.
![]()
Расчет переходных процессов с помощью операторного метода и метода моделирования.
Применим преобразование Лапласа к системе уравнений (1), сохраняя для изображения те же обозначения, что и для оригиналов, однако рассматривая их как функции переменной p. Получим:
![]()
![]()
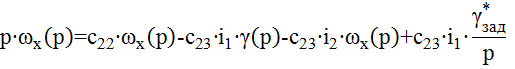
Или, преобразуя уравнение (2), получаем:

![]()
![]()
В системе уравнений (2) γзад*/р – изображение по Лапласу входного воздействия. Определитель системы (3) равен:
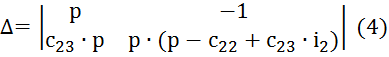
Преобразуя (4), получаем:
![]()
По правилу Крамера определяем изображение по Лапласу функции γ(t):
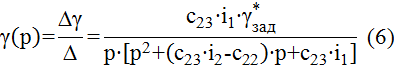
Аналогично находим изображение по Лапласу функции ωx(t):
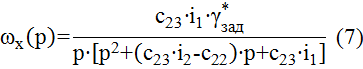
Для нахождения оригинала функции γ(p) и ωx(p) вычислим корни характеристического уравнения системы (1). Само уравнение имеет вид:
![]()
Из него находим корни:
![]()
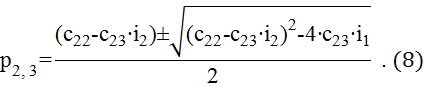
Если второй и третий корни представляют собой пару комплексно-сопряженных корней, то левую часть характеристического уравнения (8) можно представить в виде:
![]()
где:
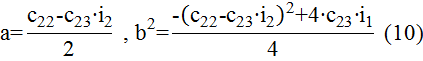
В этом случае:
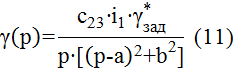
Из таблиц изображения функции по Лапласу выбираем функцию, соответствующую выражению (11):
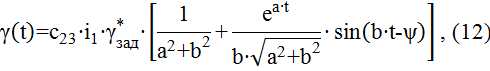
где ψ=arctg(b/a). Аналогично определяем ωx(t):
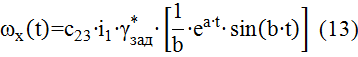
Если корни p2 и p3 – вещественные (p2=-a, p3=-b), то:
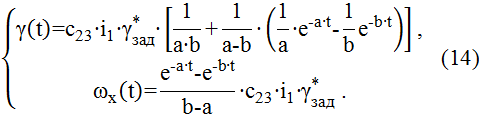
Проведем моделирование переходного процесса в системе (1).
Ниже приведен листинг программы для расчета моделирования системы.
function dy = lab4(t,y)
dy = zeros(2,1);%Создание массива
c22 = -3.5;%Объявление коэффициентов
c23 =20;
i1=0.8;%Передаточное число
i2=1.2;
gamma=10;%gamma-известная функция, задающая программу угла раскания
dy(1) = y(2);%Запись дифф. уравнений
dy(2) =c22 * y(2) + c23*(i1*(gamma-y(1))-i2*y(2));
end
[T Y] = ode45(@lab4, [0 10], [0 0]);%Интегрирование методом Рунге-Кутта с начальными параметрами
dlmwrite('rez.txt', [T Y], 'delimiter', '\t', 'precision', '%10.5f', 'newline', 'pc');%Запись результатов расчета в файл rez.txt
plot(T, Y(:,1));
xlabel('{\gamma(t)}');%Построение графиков
grid on;
figure;
plot(T, Y(:,2));
xlabel('{\omega_x(t)}');
grid on;
Далее получаем таблицу данных.
|
t, с |
γ, град |
ωх , град/с |
|
0,00000 |
0,00000 |
0 |
|
0,50205 |
2,41345 |
4,51141 |
|
1,03069 |
4,45997 |
3,29392 |
|
1,51879 |
5,85568 |
2,46407 |
|
2,00802 |
6,90185 |
1,84203 |
|
2,52197 |
7,71772 |
1,35725 |
|
3,01344 |
8,29616 |
1,01231 |
|
3,52185 |
8,74069 |
0,74879 |
|
4,01513 |
9,06083 |
0,55884 |
|
4,50704 |
9,29903 |
0,41699 |
|
5,01796 |
9,48270 |
0,30761 |
|
5,50710 |
9,61326 |
0,22997 |
|
6,02238 |
9,71534 |
0,16925 |
|
6,51404 |
9,78750 |
0,12633 |
|
7,00138 |
9,84097 |
0,09456 |
|
7,52656 |
9,88362 |
0,06924 |
|
8,01470 |
9,94295 |
0,05179 |
|
8,52144 |
9,97560 |
0,0383 |
|
9,00708 |
10,1750 |
0,02869 |
|
9,51763 |
9,96438 |
0,02118 |
|
10,00000 |
9,97327 |
0,01589 |

Далее получаем графики γ(t) и ωx(t).

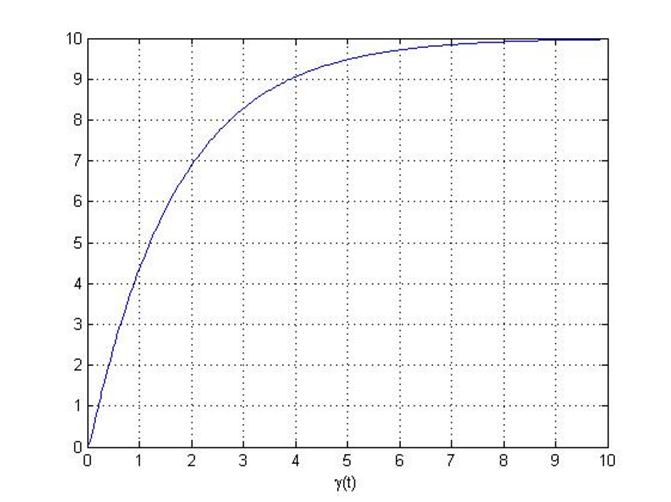

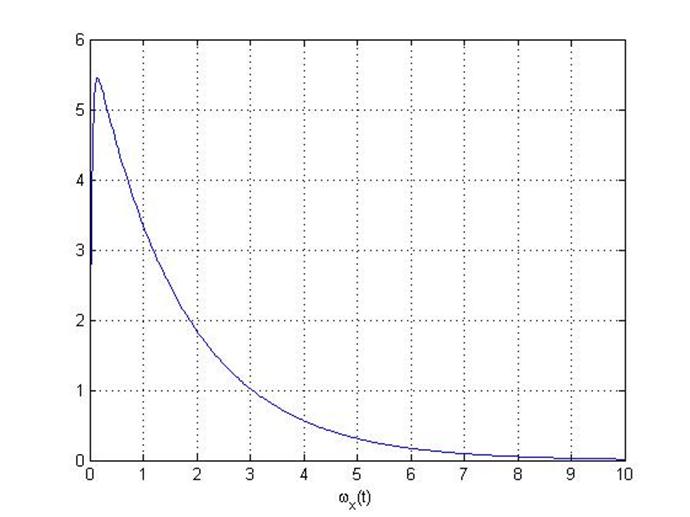
После моделирования процессов в системе (1) проведем аналитическое решение системы (1). Для этого воспользуемся системой уравнений (14) и (10). Ниже будет представлен листинг программы для вычисления γ(t) и ωx(t). В «{}» будут указаны комментарии к соответствующим блокам программы.
program Lab_5;{Программа для аналитического определения параметров gamma(t) и omega_x(t) для угла крена}
const {Объявление констант программы}
c22=-3.5;c23=20;i1=0.8;i2=1.2;
dt=0.1;{Шаг по времени}
tk=10;{Конечное время t=10 c}
gamma_zad=10;{Заданный угол gamma=10. Программное значение}
var {Объявление переменных программы}
i:integer;
t,a,b,gamma_t,omega_xt:real;
f:text;
begin
assign(f,'Rezultat.txt');{Файл вывода результатов}
rewrite(f);
writeln(f,'t,c gamma(t),град omega_x(t), град/с');
a:=0.5*(c22-c23*i2);{Корни уравнеия}
b:=sqrt(0.25*(4*c23*i1-sqr(c22-c23*i2)));
writeln(f,t:6:2,' ',gamma_t:6:2,' ',omega_xt:6:2);
i:=0;{начальные условия}
t:=0;
repeat {Цикл повтора по времени t}
gamma_t:=c23*i1*gamma_zad*((1/(a*b))+(1/(a-b))*((1/a)*Exp(-a*t)-(1/b)*Exp(-b*t)));
omega_xt:=c23*i1*gamma_zad*((1/(b-a))*(Exp(-a*t)-Exp(-b*t)));
writeln(f,t:6:4,' ',gamma_t:6:4,' ',omega_xt:6:4);
i:=i+1;
t:=i*dt;
until t>=tk;{Конец цикла по времени t}
close(f);
writeln('Расчет окончен.');
end.
Далее получили таблицу данных.
|
t, с |
γ, град |
ωх , град/с |
|
0,00 |
0,00 |
0,00 |
|
0,5 |
2,41 |
4,51 |
|
1,04 |
4,46 |
3,30 |
|
1,52 |
5,86 |
2,50 |
|
2,0 |
7,00 |
1,84 |
|
2,50 |
7,72 |
1,36 |
|
3,0 |
8,3 |
1,01 |
|
3,55 |
8,74 |
0,74 |
|
4,01 |
9,06 |
0,55 |
|
4,50 |
9,30 |
0,41 |
|
5,01 |
9,50 |
0,31 |
|
5,51 |
9,61 |
0,23 |
|
6,02 |
9,71 |
0,17 |
|
6,51 |
9,8 |
0,12 |
|
7,00 |
9,84 |
0,10 |
|
7,52 |
9,88 |
0,06 |
|
8,01 |
9,94 |
0,05 |
|
8,52 |
9,99 |
0,03 |
|
9,00 |
10,12 |
0,02 |
|
9,51 |
9,98 |
0,01 |
|
10,00 |
9,97 |
0,015 |

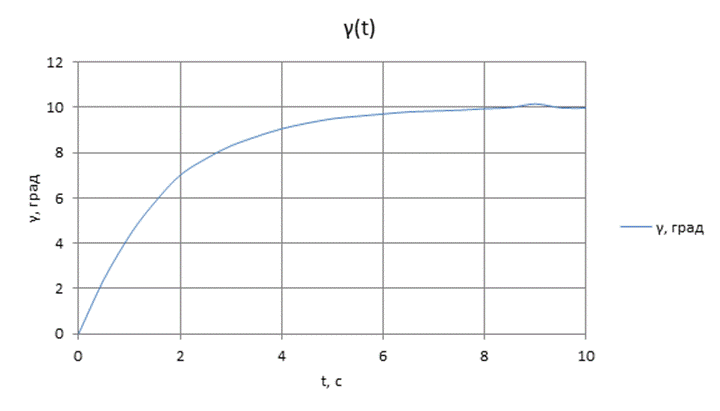

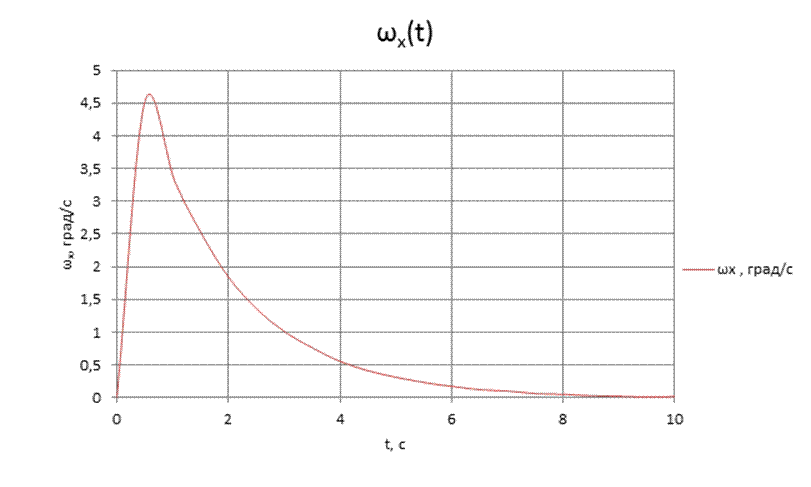
Далее определяем:
1. Время переходного процесса tп: из таблицы 1 и таблицы 2 видно, что tп=10 секунд;
2. Перерегулирование:
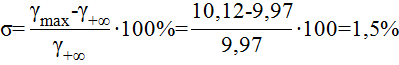
3. Время первого выброса t1=9 c.
4. Колебательность, определяемая числом колебаний за время переходного процесса: 2;
5. Установившееся значение ошибки (статическая ошибка):
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.