Балтийский Государственный Технический Университет
им Д.Ф.Устинова
«Военмех»
Кафедра А5

Лабораторная работа №2
Определение частотных характеристик замкнутой САУ.
Вариант №19
Выполнил: Каипова
Альбина, А482
Проверил: Санников
Виталий Андреевич
Санкт-Петербург, 2012
Цель работы: изучение методов определения частотных характеристик системы автоматического управления (САУ)
Основными характеристиками линейных стационарных динамических систем являются весовые функции и частотные характеристики. С помощью этих показателей могут решаться задачи анализа устойчивости и точности САУ при неслучайных и случайных воздействиях, а также задачи синтеза САУ.
Частотные характеристики определяют в установившемся режиме реакцию системы на гармоническое колебание.
Если известна передаточная функция системы Ф(р), то частотная характеристика Ф(jw) может быть найдена аналитически и представляет собой передаточную функцию при чисто мнимых значениях аргумента р=jw:
Ф(jw)=Ф(р) при р=jw
Частотная характеристика может быть найдена методами моделирования. Для этого на вход системы подается гармоническое воздействие частоты w:
f(t)=f0sin(wt)
реакция системы после окончания переходного процесса представляет собой также передаточную функцию:
x(t)=x0sin(wt+φ)
отличающуюся от входной функции по амплитуде и фазе, но имеющую ту же частоту. Схема моделирования показана на рис.2.1

![]()
![]() f(t)=f0sin(wt)
x(t)=x0sin(wt+φ)
f(t)=f0sin(wt)
x(t)=x0sin(wt+φ)
рис.2.1
частотная амплитудно-фазовая характеристика системы или комплексный коэффицииент усиления системы:
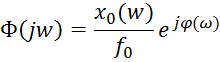
Здесь x0(w) и f0 – амплитуды выходной реакции системы и входного
воздействия, ![]()
- разность фаз выходной реакции и входного воздействия. При моделировании частота w изменяется дискретно от 0 до достаточно большогоо значения wmax , которое определяется из физических соображений.
Выражение для Ф(jw) может быть представлено в виде:
Ф(jw)=A(w)ejφ(w)
Или в виде
![]()
Здесь А(w) – амплитудная частотная характеристика, равная отношению амплитуд выходного и входного гармонических сигналов:
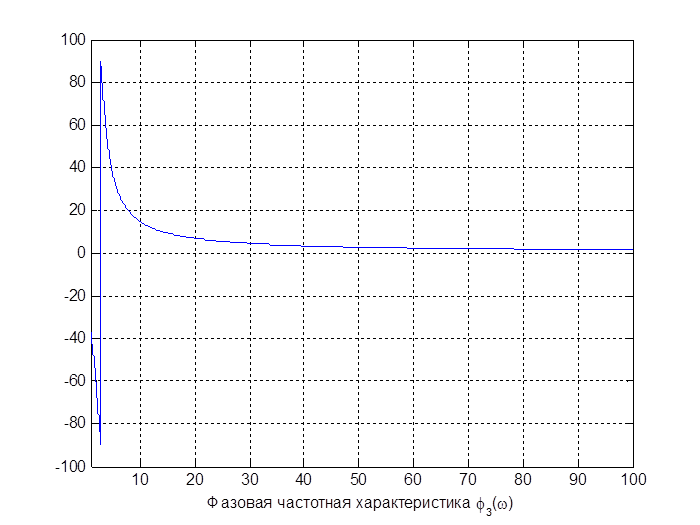
φ(w) – фазовая частотная характеристика,
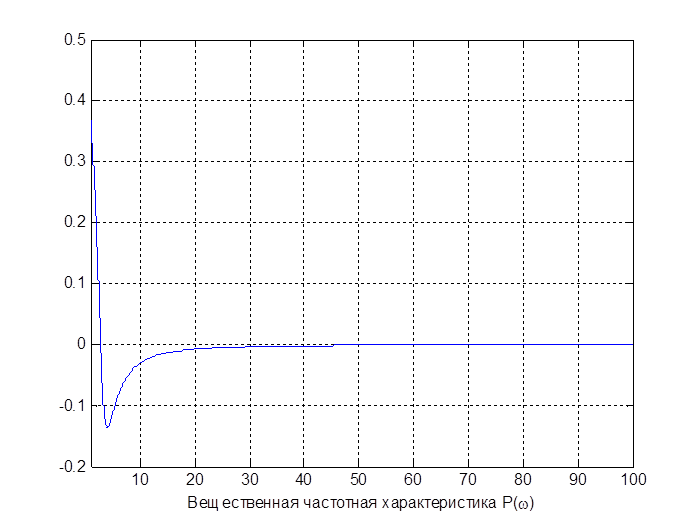
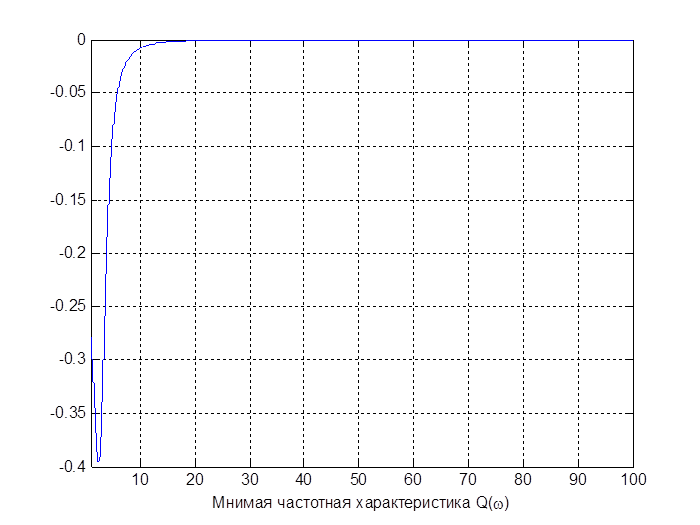
P(w)- вещественная частотная характеристика, Q(w) – мнимая частотная характеристика.
Для получения частотных характеристик экспериментальным путем для каждого значения частоты определяют амплитуду гармонического воздействия, амплитуду выходной величины, а также ыазовый сдвиг между обоими колебаниями. Частотные характеристики могут быть получены как для замкнутых, так и для разомкнутыхзвеньев системы.
Описание работы и исходные данные
Рассмотрим систему стабилизации углового движения ЛА относительно ц.м. в продольной плоскости. В качестве программного движения принимается полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения.
1)
![]()
2)
![]()
3)
![]() =
=![]()
4)
![]()
2.1
где ![]() – угол атаки,
– угол атаки, ![]() - угол тангажа,
- угол тангажа, ![]() - угловая скорость тангажа,
- угловая скорость тангажа, ![]() -угол отклонения руля высоты,
-угол отклонения руля высоты, ![]() – известные динамические коэффициенты, i1,i2 – передаточные числа,
– известные динамические коэффициенты, i1,i2 – передаточные числа, ![]() -известная функция, задающая программу угла тангажа.
-известная функция, задающая программу угла тангажа.
в системе
уравнений индекс ![]() отклонений от программных значений опущен. Уравнения 1)-3)
описывают динамику ЛА, уравнение 4) – уравнение системы управления. При этои
рулевая машина считается безынерционной.
отклонений от программных значений опущен. Уравнения 1)-3)
описывают динамику ЛА, уравнение 4) – уравнение системы управления. При этои
рулевая машина считается безынерционной.
![]()
![]()
![]()
![]() Системе уравнений соответствует
структурная схема системы стабилизации угла тангажа.
Системе уравнений соответствует
структурная схема системы стабилизации угла тангажа.![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Рис.2.2
Передаточная
функция ЛА, характеризующая передачу воздействия от входа![]()
до выхода ![]() , имеет вид
, имеет вид
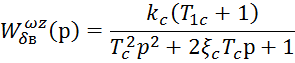
Где
![]() – коэффициент усиления ЛА
– коэффициент усиления ЛА
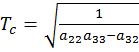 – постоянная времени ЛА
– постоянная времени ЛА
![]() – коэффициент демпфирования
– коэффициент демпфирования
![]() – постоянная
времени форсирующего звена.
– постоянная
времени форсирующего звена.
Для получения передаточной функции необходимо применить преобразования Лапласа к системе и решить полученную систему алгебраических уравнений.
Численные значения коэффициентов.
Исходные данные:
|
вариант |
|
|
|
|
|
|
|
19 |
-1.3 |
-3.0 |
-0.8 |
2.9 |
1.6 |
0.5 |
Задача 1.2.
Частотные характеристики исследуемой динамической системы, описываемой дифференциальными уравнениями 2.1 , рассчитываются теоретически или определяются экспериментальными методами.
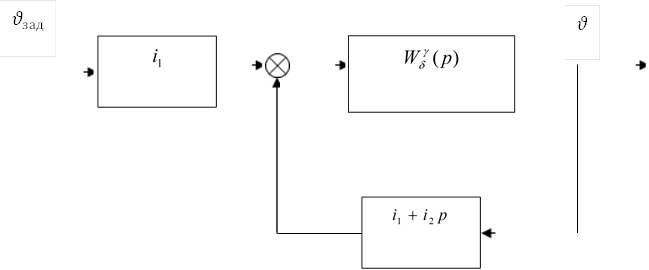
Рассмотрим способ расчета частотных характеристик. Структурную схему системы стабилизации угла тангажа 2.2 представим в виде рис.2.3
 |
-
Рис2.3
Здесь
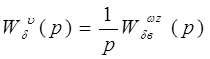 .
.
Тогда передаточная функция замкнутой САУ с отрицательной обратной связью определяется соотношением:
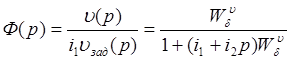
После подстановки этих выражений передаточная функция приводится к виду
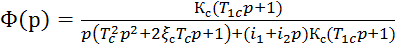 (*)
(*)
При вычислении
амплитудно-фазовой характеристики замкнутой САУ в формулу * вместо ![]() подставляем
подставляем ![]() и
приводим частотную характеристику передаточную функцию к виду:
и
приводим частотную характеристику передаточную функцию к виду:
![]()
где
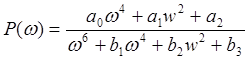
-вещественная частотная характеристика;
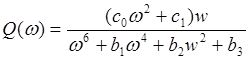
-мнимая частотная характеристика.
Здесь:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Амплитудная и фазовая частотная характеристика замкнутой САУ определяются с помощью выражений :
![]() ,
,
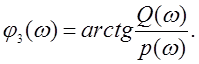
Амплитудная частотная характеристика определяется также моделированием.
При исследовании
реальных динамических систем на выход системы подается гармоническое
воздействие. В работе рассматривается математическая модель. Для определения
амплитуды ![]() моделированием на ЭВМ воздействие
моделированием на ЭВМ воздействие ![]() заменяется гармонической функцией
заменяется гармонической функцией ![]() Система дифференциальных уравнений
принимает следующий вид:
Система дифференциальных уравнений
принимает следующий вид:
5)
![]()
6)
![]()
7)
![]() =
=![]()
8)
![]()
Для решения системы методом Рунге-Кутта используется программа, она решает при десяти значениях частоты гармонических колебаний. Частота изменяется дискретно с постоянным шагом, равным начальному значению частоты колебаний.
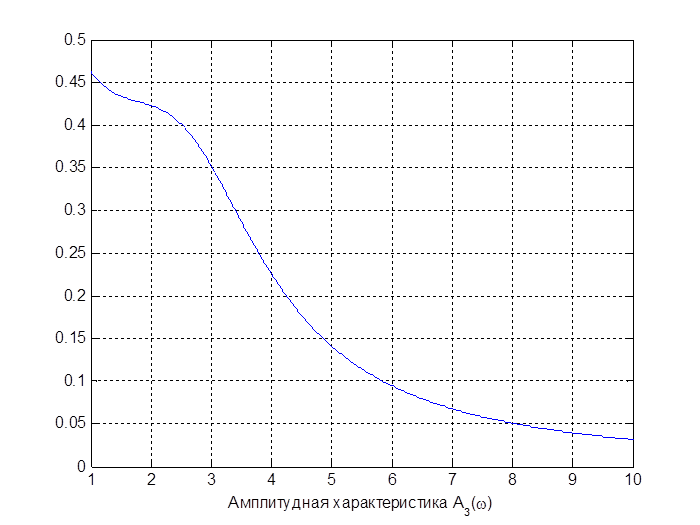
Амплитудная характеристика:
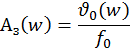
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.