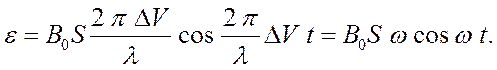Электричество и электрическая железная дорога. Конспект лекций по физике, страница 42

                (15.5)

В рамке действует переменная ЭДС и течет переменный ток с циклической частотой 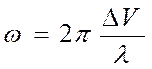. По закону Ома амплитуда силы переменного тока равна отношению ЭДС к полному сопротивлению рамки: 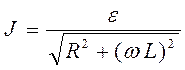, где R –– активное сопротивление,  –– индуктивное сопротивление воображаемой рамки.

Согласно закону Ампера сила тяги одной рамки равна , где b – длина активного участка рамки, равная ширине шины. Подставив амплитудное значение силы тока и ЭДС из (15.5), получим для силы тяги формулу

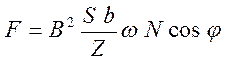  .                                      (15.6)

Здесь N –– число воображаемых рамок на шине или число троек тяговых электромагнитов экипажа. φ – сдвиг фаз между силой тока и ЭДС, 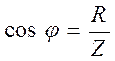, обусловлен индуктивностью рамки.

Контрольные вопросы

1. Объясните причину аэродинамического сопротивления движению тела в воздухе. Запишите формулу для силы сопротивления.

2. Объясните физический принцип электродинамического способа левитации экипажа ВСНТ, как обусловленный силами взаимодействия рамки с переменным током на экипаже и токопроводящей путевой шиной.

3. Оцените добавочное давление воздуха под днищем экипажа массой 10 тонн при площади 25 м², чтобы экипаж висел над дорожным полотном. Будет ли устойчивым такой подвес?

4. Оцените площадь крыльев экипажа ВСНТ массой 10 тонн, если коэффициент подъемной силы 0,3 скорость100 м/с.  Если использовать эффект экранирования, то коэффициент возрастает в три раза. Может достаточно площади днища для полета?

5. Является ли устойчивым движение при электромагнитном подвесе экипажа ВСНТ?

6. Оцените выгоды высокоскоростного транспорта, если между городами расстояние 100 км скорость экипажа 400 км/час,  время в городском транспорте 1 час.

7. Почему для получения сильных магнитных полей необходимо охлаждение обмоток электромагнитов до сверхпроводящего состояния?  Существует ли ограничение на силу тока  в сверхпроводниках и на индукцию магнитного поля?

16. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Любая электрическая цепь обладает индуктивностью, электрической емкостью и активным сопротивлением. В такой цепи возможны собственные электрические колебания. Если пренебречь затуханием, то период колебаний определяется формулой Томсона .

Подключение электрической цепи к генератору переменного напряжения приводит к возникновению в цепи переменного электрического тока. Это ток,  который изменяется по величине и по направлению. Переменный ток  может рассматриваться как вынужденные колебания силы тока, заряда, напряжения в цепи под действием генератора.

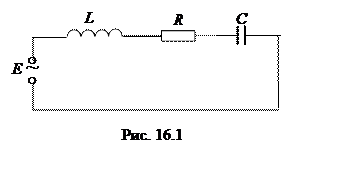
Пусть электрическая цепь состоит из соединенных последовательно катушки индуктивностью L, резистора с сопротивлением Rи конденсатора емкостью C, которая подключена к генератору переменного тока (рис. 16.1).   Пусть   ЭДС генератора изменяется по гармоническому закону:  ,  где ω – циклическая частота генератора.  Чтобы определить силу тока в цепи, применим второе правило Кирхгофа к контуру: сумма падений напряжения на конденсаторе   и резисторе JR  равна алгебраической сумме ЭДС генератора ε  и ЭДС самоиндукции катушки  :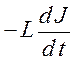

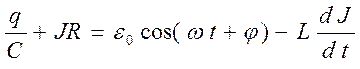.                           16.1

Здесь q и J – мгновенные значения заряда конденсатора и силы тока в цепи. Из опыта известно, что при действии внешней переменной силы колебательная система совершает вынужденные колебания с частотой вынуждающей силы. Собственные колебания рано или поздно затухают. Частное решение уравнения  (16.1) будем искать в виде гармонической функции силы тока с частотой переменной ЭДС:

 J =J₀ coswt.                                               16.2

Подставив функции для заряда и производной по току в уравнение (16.1) по соотношениям: 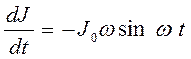 ;  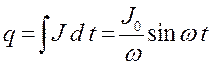,  получим

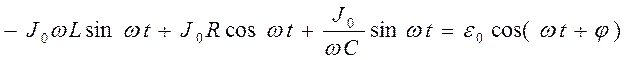.             16.3

2. В уравнении (16.3) два неизвестных: амплитуда силы тока J₀и сдвиг фаз между током и напряжением j.  Для их определения воспользуемся геометрическим методом векторных диаграмм, как это делается при сложении колебаний одинаковой частоты. Проведем из полюса векторы,  длины которых равны амплитудам  уравнения (16.3), под углом к оси напряжений, равным начальным фазам (рис. 16.2). Если эти векторы поворачивать против часовой стрелки с угловой скоростью, равной циклической частоте колебаний, то проекции векторов на ось напряжений будут совпадать с членами уравнения (16.3).

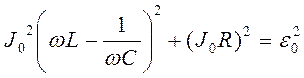Запишем  теорему Пифагора для заштрихованного  треугольника . Откуда амплитуда тока  равна