Электричество и электрическая железная дорога. Конспект лекций по физике, страница 20

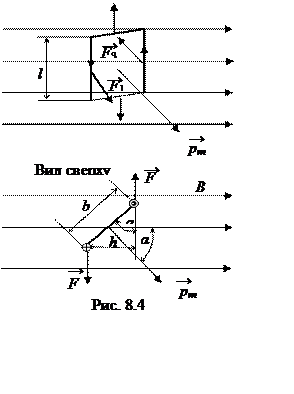
4. Рамка с током в магнитномполе. Пусть в однородном магнитном поле находится прямоугольная рамка с током силой J, как показано на рис. 8.4. На горизонтальные стороны рамки действуют силы, которые пытаются деформировать рамку в вертикальном направлении. На боковые вертикальные стороны рамки действуют силы, создающие момент сил  . Подставив формулу силы Ампера, получим  .  Произведение длины рамки на ширину является площадью рамки. Произведение силы тока на площадь рамки назовем магнитным моментом рамки   .  Направление вектора магнитного момента определяется правилом буравчика: если ручки буравчика вращать по току в рамке, то магнитный момент направлен по перемещению буравчика.

Момент сил, вращающий рамку в магнитном поле, равен произведению магнитного момента на вектор индукции поля:

                                               8.5

или в векторном виде:  

Момент сил поворачивает рамку так, чтобы плоскость рамки стала перпендикулярно силовым линиям, а вектор магнитного момента повернулся к силовым линиям поля. Это положение устойчивого равновесия рамки, при котором силы Ампера растягивают рамку. Сумма сил равна нулю.

Если в магнитном поле находится плоская катушка из Nвитков площадью S, то её магнитный момент равен

.                               8.6

Рамка в магнитном поле обладает потенциальной энергией. Её можно определить через работу момента сил Ампера по повороту рамки: . Полагая постоянную интегрирования равной нулю, получим

 или    .          8.7

Минимум потенциальной энергии рамки будет в положении равновесия,  α=0.

Если магнитное поля является неоднородным, то силы Ампера, действующие на рамку, кроме вращающего момента создают результирующую силу. По формуле связи силы и потенциальной энергии  проекция силы равна первой производной от энергии по координате с обратным знаком:

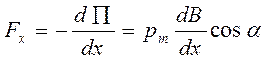 .                                          8.8

В магнитном поле рамка с током поворачивается так, чтобы вектор магнитного момента был направлен вдоль силовых линий и затем  притягивается к области  усиления поля.

5. Сила Лоренца. По гипотезе Лоренца сила, действующая на проводник с током в магнитном поле, есть результирующая сил, действующих на электрические заряды, создающие ток. Поделим силу Ампера на число зарядов в отрезке проводнике длиной l: 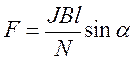 .  Определим силу тока как отношение суммарного заряда   ко времени 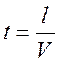 дрейфа заряда от начала до конца проводника 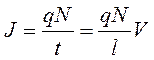. Подставим силу тока и получим формулу

,   или  в векторном виде  .               8.9

Сила Лоренца направлена всегда перпендикулярно вектору скорости частицы и силовым линиям магнитного поля. Для положительно  заряженной частицы направление силы определяется правилом левой руки: силовые линии входят в ладонь, четыре пальца по скорости, отогнутый большой палец укажет направление силы. Для отрицательной частицы – наоборот.  Сила Лоренца работы над частицей не совершает, следовательно, кинетическую энергию и скорость частицы не изменяет.

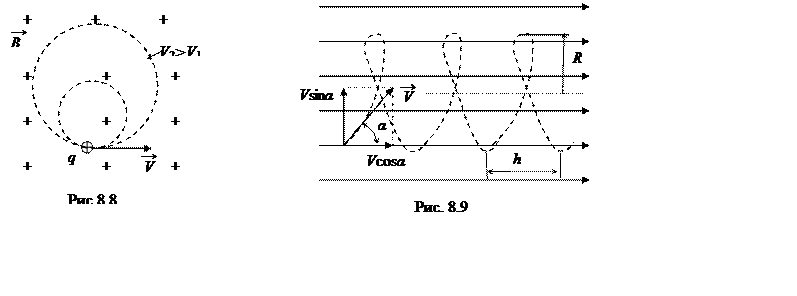
6. Движение частиц в однородном магнитном поле. Пусть частица влетает в однородное магнитное поле перпендикулярно силовым линиям (рис. 8.8). Сила Лоренца является центростремительной силой. Частица будет двигаться по дуге окружности. Второй закон Ньютона в проекции на нормаль имеет вид 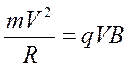  . Откуда радиус кривизны траектории равен

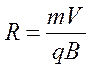.                                                   8.10

Период обращения по окружности 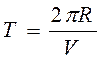 . Подставив формулу радиуса орбиты, получим

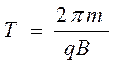.                                              8.11

Период обращения не зависит от скорости движения частицы.

Если частица влетает под углом α к силовым линиям однородного поля, то движение можно представить в виде двух движений: движение с перпендикулярной компонентой скорости по окружности и  поступательное движение вдоль силовых линий  со скоростью  . Траектория будет винтовой линией (рис. 8.9) с радиусом и шагом

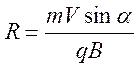       и 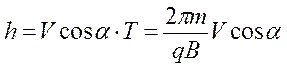   .                                                   8.12

Магнитное поле Земли отклоняет потоки заряженных космических частиц. Навиваясь на силовые линии поля, они отклоняются к полюсам, вызывая там при входе в атмосферу полярные сияния.