Электричество и электрическая железная дорога. Конспект лекций по физике, страница 2

5. Если поле создается не одним, а несколькими точечными зарядами, то вектор результирующей напряженности определяется, согласно принципу суперпозиции сил, векторной суммой напряженностей полей отдельных зарядов: .  Если заряды распределены непрерывным образом по объёму тела, либо по поверхности, либо по длине, то выбирается малый заряд dq, который можно считать точечным и суммарная напряженность определяется векторным интегралом: . Здесь  вектор  напряженностей поля малого зарядов 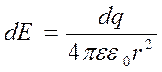 направлен по радиус-вектору для поля положительного заряда и в обратном направлении для отрицательного заряда.  Для получения скалярных уравнений векторные суммы и интегралы проецируются на оси координат.

6. Для наглядности электростатическое поле изображают с помощью силовых линий. Это линия в пространстве, касательные к которой совпадают с вектором напряженности. Линии начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, либо уходят в бесконечность. Густота силовых линий пропорциональна напряженности поля  (рис.2).

7. В некоторых задачах с симметричным расположением электрического заряда на телах можно заранее предсказать распределение напряженности в пространстве. В этом случае становится удобным для расчета напряженности применение теоремы Гаусса.

Введем  понятие потока вектора напряженности как скалярного произведения вектора напряженности на вектор элементарной площадки, которую пронизывают силовые линии поля,. Здесь угол  α – угол между вектором напряженности и вектором  площади, который направлен по нормали к площадке. Поток пропорционален числу силовых линий, пронизывающих площадку. 

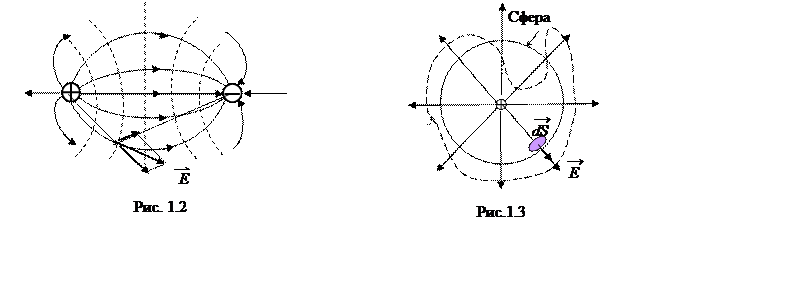Определим поток вектора напряженности сквозь сферу произвольного радиуса, в центре которой поместим точечный заряд, как интеграл от элементарного потока напряженности  . Силовые линии направлены радиально от заряда и пронзают элементы сфера по нормали к их поверхности, то есть cos α=1 (рис.3).  Величина вектора напряженности одинакова во всех элементах сферы.  Вынесем напряженность за знак интеграла . Интеграл, то есть сумма элементарных площадок, будет равна площади сферы 4πrR². Подставим формулу напряженности поля точечного заряда 1.3. В результате поток вектора напряженности будет .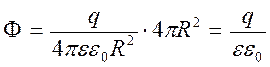

Обобщим полученный результат на произвольную замкнутую поверхность (пунктир на рис. 1.4). Число силовых линий, пронзающих её такое же, как и через сферу. Значит, потоки напряженности будут одинаковы. Во-вторых, если внутри имеется не один заряд, а несколько, то потоки напряженностей от зарядов по принципу суперпозиции складываются. В итоге, в общем случае теорема Гаусса имеет вид

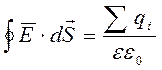.                                                   1.4.

Поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхности равен отношению алгебраической суммы зарядов внутри поверхности к абсолютной диэлектрической проницаемости среды.

Количество задач, решаемых с помощью теоремы Гаусса невелико. Поверхность интегрирования выбирается так, чтобы на одних участках поверхности вектор напряженности был постоянен, на других вектор напряженности скользил бы, не пронизывая поверхность, и поток через неё был бы равен нулю.

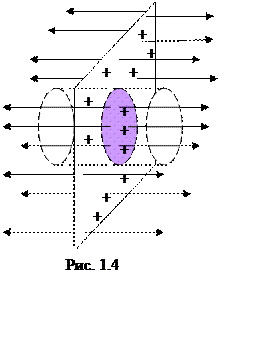8. Например, рассчитаем напряженность бесконечной плоскости, заряженной равномерно с поверхностной плотностью заряда  σ  (рис. 1.4). Выберем поверхность интегрирования в форме цилиндра, торцы которого расположены по обе стороны плоскости, параллельно ей. Поле бесконечной плоскости однородное. Поток выходит из обоих торцов цилиндра и равен 2ES. Поток через боковую поверхность цилиндра равен нулю. Электрический заряд внутри цилиндра сосредоточен на диске, вырезанном цилиндром (на рис. 1.4 затенен). Он равен произведению поверхностной плотности заряда на площадь диска σS.  По теореме Гаусса 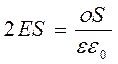. Оттуда напряженность поля заряженной равномерно плоскости вблизи её середины равна

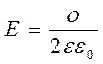 .                                                  1.5

Если рядом расположены две пластины, заряженные разноименно с одинаковой плотностью заряда, то напряженности поля между ними складываются: 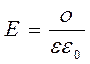, а снаружи вычитаются E=0.