Электричество и электрическая железная дорога. Конспект лекций по физике, страница 37

1. Для электрической железной дороги выполняется закон Ома. Напряжение подстанции равно сумме противо-ЭДС двигателей и потере напряжения на проводах контактной сети и обмоток двигателя: . Однако определить силу тока в контактной сети непосредственно по уравнению закона Ома невозможно. Это обусловлено тем, что  противо-ЭДС не постоянна, а зависит от индукции магнитного поля В:  для одного двигателя. В двигателях последовательного возбуждения противо-ЭДС будет зависеть от силы тока двигателя точно также как и индукция (рис. 14.1). Суммарную противоЭДС двигателей локомотива определяют сложением ЭДС отдельных двигателей в зависимости от схемы соединения двигателей.

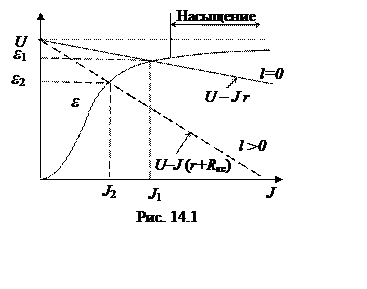Возможно графическое решение уравнения закона Ома. Пусть для простоты двигатели электровоза при равномерном движении вращаются с постоянной угловой скоростью ω. Проведем на графике (рис. 14.1) прямые линии . Абсциссы точек пересечения с линией ЭДС всех двигателей локомотива дадут расчетное значение силы потребляемого тока. Так как сопротивление контактной сети зависит от расстояния между подстанцией и электровозом l >0, то с удалением от подстанции угол наклона линии  будет возрастать, точка пересечения будет смещаться в диапазон малых токов. Определив силу тока, можно определить мощность тяговых двигателей  как площадь прямоугольника (P=εJ) на графике.

2. На стадии проектирования электровоза необходимую силу токаможноопределить по заданной мощности тяговых двигателей. Зависимость полезной мощности тяговых двигателей от силы тока, согласно уравнению баланса мощности, определяется уравнением второго порядка

 .                                      14.1

Функция мощности имеет максимум (рис.14.2). Приравняв первую производную к нулю 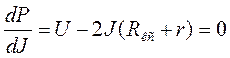, получим значение силы тока, при котором полезная мощность принимает максимальное значение

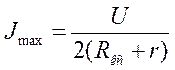 .                                                  14.2

Это в два раза меньше тока короткого замыкания, когда  якоря  двигателей не вращаются, противоЭДС отсутствует.  Однако работать в этом режиме тяговые двигатели не должны, так как  коэффициент полезного действия подстанции 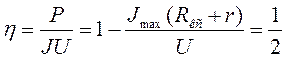   слишком мал,  равен 50 %.

Решая квадратное уравнение баланса мощности, подставив в него  J_maxи  приведя к виду 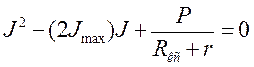 можно определить силу тока, потребляемую двигателями локомотива.  Это уравнение второго порядка относительно силы тока и его решение имеет два корня:

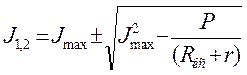.                                     (14.3)

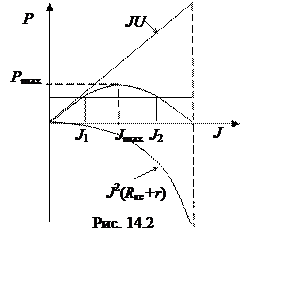
Если корни действительные и положительные, то двигатели локомотива выбирают меньший ток J₁. Если корни мнимые, то тяговая подстанция не в состоянии обеспечить заданную мощность тяговых двигателей локомотива из-за большого сопротивления контактной сети. Следует или увеличивать сечение проводов контактной сети, или уменьшать расстояние между подстанциями.

Однако на рассчитанное предельное значение силы тока тяговых двигателей накладываются несколько ограничений, которые нельзя превышать. Сила тока не может быть настолько большой, чтобы ведущие колеса локомотива буксовали (см. формулу 13.1: 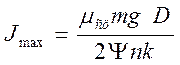). Необходимо, чтобы КПД подстанции был не менее 95%, необходимо, чтобы не перегревались двигатели, не перегревался провод.

3. Потребуем, чтобы КПД тяговой подстанции был не менее η=95%,  то есть тепловые потери не превышали 5% от потребляемой мощности.  По закону Джоуля –Ленца мощность тепловых потерь равна произведению квадрата силы тока на сопротивление . Отсюда допустимая сила тока по ограничению потерь мощности равна

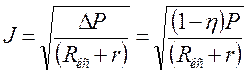.                                              14.4

Расчетная сила тока по этой формуле  не должна превышать силу тока формуле 14.2 , иначе КПД железной дороги будет мал.

Исключим из закона Джоуля-Ленца силу тока по формуле КПД подстанции   . Мощность тепловых потерь будет равна

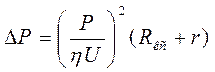                                           14.5

Как видно из формулы, для снижения тепловых потерь, следует, во-первых, уменьшать сопротивление проводов контактной сети. По формуле 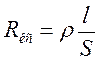 нужно  увеличить площадь сечения, но это приведёт к утяжелению проводов, удорожанию контактной сети. Или следует уменьшать  длину контактного провода, то есть уменьшать расстояние между подстанциями.