Электричество и электрическая железная дорога. Конспект лекций по физике, страница 15

В режиме короткого замыкания  при отсутствии нагрузки, когда  R = 0, вся теплота выделяется на внутреннем сопротивлении и полезная мощность равна нулю  (рис. 6.3).  С  увеличением сопротивления нагрузки, пока  R<<r, полезная мощность возрастает почти прямо пропорционально сопротивлению R.  С дальнейшим возрастанием сопротивления нагрузки наступает ограничение силы тока, и мощность,  достигнув максимума, начинает спадать.  При больших значениях сопротивления нагрузки  (R>>r), мощность уменьшается обратно пропорционально сопротивлению, стремясь к нулю при разрыве цепи.

Максимум мощности соответствует условию равенства нулю первой производной от тепловой мощности по сопротивлению. Продифференцировав (4), получи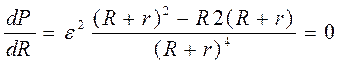м .  Отсюда следует, что полезная мощность максимальна, если  R = r. Подставив  в (6.4), получим  .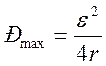

Работа источника тока характеризуется коэффициентом полезного действия.  Это, по определению, отношение полезной работы к полной работе источника тока: 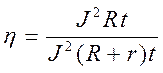.  После сокращения  формула КПД примет вид

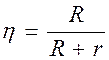.(6.5)

В режиме короткого замыкания при R= 0,  КПД равен нулю, так как нет нагрузки (рис. 6.3). С ростом сопротивления нагрузки  КПД растет и стремится к 100% при больших значениях сопротивлениях (R>>r).

6.  Расчет сил токов и напряжений в сложных разветвленных цепях с помощью закона Ома может оказаться достаточно сложным.  Правила Кирхгофа позволяют упростить решение задачи.

Согласно первому правилу Кирхгофа алгебраическая сумма сил токов, сходящихся в узле равна нулю:

.                                           6.6

Узлом называется точка электрической цепи, в которой сходится не менее трех проводников. Первое правило является следствием закона сохранения электрического заряда. Стоит нарушиться балансу входящих и выходящих из узла зарядов, как потенциал узла изменится, что приведет к изменению сил токов и выполнению первого правила Кирхгофа. Число узлов в электрической цепи, для которых составляются уравнения по первому правилу, должно быть на единицу меньше общего числа узлов.

Для вывода второго правила Кирхгофа применим уравнение закона Ома для участка цепи, содержащего источник тока  (рис. 6.4). Разность потенциалов между концами участка равна разности ЭДС и падения напряжения на резисторе и на внутреннем сопротивлении источника тока:  . Откуда

.                                         6.7

Запишем для контура на рис. 6.5, выделенного из какой-то разветвленной цепи, уравнения закона Ома для всех ветвей. Обход против часовой стрелки.

;     ;   . Сложим уравнения, при этом потенциалы узлов попарно сократятся. Получим уравнение второго правила Кирхгофа:  алгебраическая сумма падений напряжений в контуре равна алгебраической сумме ЭДС в этом контуре:

.                                        6.8

Порядок расчета следующий: выбрать произвольно направления токов в ветвях, выбрать направление обхода. Если направление обхода участка совпадает с направлением тока, считать ток положительным, и наоборот.  ЭДС  считать положительной, если при обходе  потенциал  повышается. При составлении уравнений для каждого следующего контура должен входить ток, не записанный в предыдущих уравнениях, то есть новая ветвь. Вместе с уравнениями по первому правилу Кирхгофа общее число уравнений должно совпадать с числом токов, с числом ветвей.

Контрольные вопросы

1. Если аккумулятор замкнуть накоротко, то чему будет равна разность потенциалов между полюсами аккумулятора? Как определить силу тока и теплоту в этом случае?

2. Когда больше разность потенциалов между полюсами источника при разряде или при зарядке током одинаковой силы?

3. Три одинаковых источника соединяются либо последовательно, либо параллельно. Определить ЭДС батарей и внутреннее сопротивление в каждом случае.

4. Металлический диск вращается с большой скоростью. Магнитное поле отсутствует. Определить направление тока в проводнике, который замыкает центр диска с периферией.

5. Лампочку, на которой написано 99 Вт, 3.6 В, подсоединяют к батарейке карманного фонарика с ЭДС з,6 В. Будет ли светиться лампа?