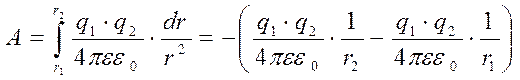Электричество и электрическая железная дорога. Конспект лекций по физике, страница 4

.                    2.1

Как видно, работа не зависит от формы  траектории, а только от положения движущегося заряда в начале и в конце движения, На замкнутой траектории (r₂=r₁) работа будет равна нулю.  То есть, электростатическое поле является потенциальным полем, а кулоновские силы – консервативными силами.

2. Обобщая для поля произвольного числа зарядов, работу сил электростатического поля  по замкнутой траектории  следует также приравнять к нулю: .  Интеграл по замкнутой траектории от скалярного произведения вектора на элемент длины  называется циркуляцией вектора.  Итак, для электростатического поля циркуляция напряженности электростатического поля равна нулю. И наоборот, если циркуляция напряженности  равна нулю, то такое поле является электростатическим.  Это связано с тем, что силовые линии электростатического поля начинаются и кончаются на зарядах и  не замкнуты.  Иначе циркуляция, определенная по контуру, совпадающим с замкнутой силовой линии, будет отлична от нуля.

3. По формуле связи работы и потенциальной энергии, , из уравнения 2.1 следует, что потенциальная энергия взаимодействия двух точечных зарядов определяется формулой:

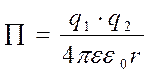.                                                     2.2

Отношение потенциальной энергии 2.2 пробного заряда q₂ к  величине его заряда не зависит от заряда и является энергетической характеристикой источника поля, называемой потенциал: 

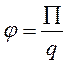 .                                              2.3

Соответственно потенциальная энергия заряда равна произведению заряда на потенциал: . Если поле создано точечным зарядом q, то потенциал некоторой точки поля на расстоянии r, определяется формулой

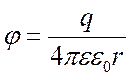.                                              2.4

Если поле создается системой зарядов, то по принципу суперпозициипотенциал поля равен сумме потенциалов полей отдельных зарядов: 

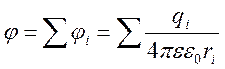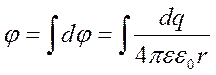,        или       .                                2.5

Работу по перемещению заряда в электростатическом поле можно определить как произведение величины заряда на разность потенциалов конечной и исходной точек траектории или на напряжение U:

.                                           2.6

При движении заряженной частицы в электростатическом поле сохраняется энергия: сумма кинетической и потенциальной энергии постоянна: 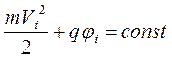 . Единицей измерения потенциала и напряжения является вольт, .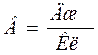

5. Между двумя характеристиками поля, напряженностью  и  потенциалом существует связь, которую можно установить, определив элементарную работу при перемещении заряда вдоль силовой линии (рис. 2.2).  Работа силы  F = qE на пути dl  вдоль силовой линии  совершается полем за счёт убыли потенциальной энергии взаимодействия:  qEdl = – qdj.   Отсюда

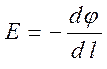          .                                                   (2.7)

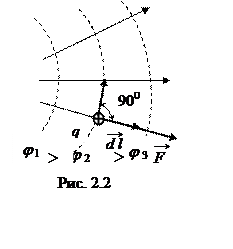
Напряженность электростатического поля равна быстроте изменения потенциала вдоль силовой линии и как вектор направлена в сторону уменьшения потенциала. Производная  от потенциала по координате, направленной по силовой линии в сторону повышения потенциала, 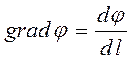  называется градиентом потенциала. То есть   .

6. Для наглядности электростатическое поле изображают с помощью эквипотенциальных поверхностей. Это поверхности равного потенциала.  Силовые линии и эквипотенциальные  поверхности электростатического  поля ортогональны, то есть их касательные взаимно  перпендикулярны. Доказать это можно,  определив работу поля по перемещению заряда  по эквипотенциальной поверхности (рис. 2.2).   Так как при перемещении заряда  вдоль  эквипотенциальной поверхности  dj = 0,  то левая часть уравнения тоже равна нулю, значит cosa = 0,  то есть угол между вектором напряженности и   касательной к эквипотенциальной поверхности  равен 90 ⁰.

7. Потенциальная энергия  двух точечных  электрических зарядов может быть определена как произведение одного из зарядов, на потенциал поля второго заряда в точке, где находится первый заряд  . Или наоборот:  . Возьмем, для симметрии итоговой формулы, по половинке каждого выражения и сложив, получим энергию взаимодействия двух точечных зарядов: