Электричество и электрическая железная дорога. Конспект лекций по физике, страница 28

Отношение магнитного момента электрона к моменту импульса называется гиромагнитным отношением. Для орбитального движения оно равно половине отношения заряда к массе: 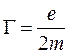 .  Однако в экспериментах Эйнштейна – де-Гааза  было обнаружено гиромагнитное отношение в два раза больше. Была предложена гипотеза, что кроме орбитального магнитного момента электрон обладает еще, так называемым, спиновым магнитным моментом. Результирующий магнитный момент атома равен векторной сумме орбитальных и спиновых магнитных моментов электронов. Так как магнитные моменты электронов в многоэлектронном атоме могут попарно компенсироваться, то результирующий магнитный момент атомов принимает значения от нуля до двух–трёх магнетонов Бора.

2.  В магнитном поле на атом, который обладает магнитным моментом, действует момент силы  , который стремится повернуть направление вектора магнитного момента вдоль силовых линий магнитного поля. Поворот векторов магнитных моментов атомов вещества при включении внешнего магнитного поля называется процессом намагничивания вещества. Характеристикой процесса намагничивания служит вектор намагничивания или намагниченность. Он равен отношению векторной суммы магнитных моментов атомов в элементарном   объёме вещества к этому объёму:

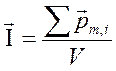.                                                11.1

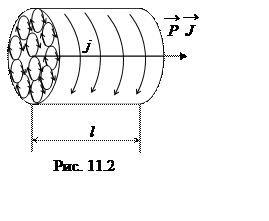
Рассмотрим намагниченный цилиндр длиной lи площадью торца S(рис. 11.2). Из рисунка видно, что орбитальные токи внутри цилиндра вычитаются, и по поверхности цилиндра как бы течет поверхностный ток,  Если на единицу длины сила тока равна j, то на всей длине jl.  Этот ток обуславливает возникновение магнитного момента цилиндра .  С другой стороны, по определению намагниченности магнитный момент цилиндра равен произведению вектора намагничивания на объем:  . Сопоставляя две формулы магнитного момента цилиндра, видно, что намагниченность численно равна линейной плотности поверхностного тока  .

3. Рассмотрим закон полного тока, но учтем магнитные свойства вещества в уравнении закона не величиной относительной магнитной проницаемости μ: 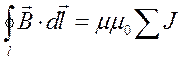 . а вектором намагниченности Ι. Для этого алгебраическую сумму токов представим в виде суммы токов проводимости катушки и поверхностных токов сердечника: 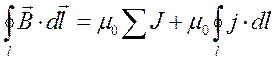.  Заменим силу поверхностного тока равным вектором намагниченности и объединим интегралы 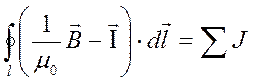  . Теперь под знаком интеграла стоит параметр магнитного поля, называемый напряженностью: 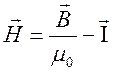 . Это расчетный параметр магнитного поля, он зависит только от токов проводимости. Закон полного тока для напряженности принимает вид

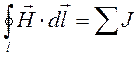  ,                                                     11.2

циркуляция вектора напряженности магнитного поля по произвольному контуру  равна алгебраической сумме токов, пронизывающих поверхность контура.

Силовая характеристика магнитного поля в веществе – индукция, определяется суммой индукции внешнего магнитного поля и индукции внутреннего магнитного поля, созданного атомами вещества:

.                                                     11.3

В  веществах, кроме ферромагнетиков, намагниченность достигает насыщения в недостижимо сильных магнитных полях. В реальных полях намагниченность  пропорциональна напряженности . Здесь χ – магнитная восприимчивость вещества. В однородном изотропном веществе индукция магнитного поля пропорциональна напряженности:  .

4. По магнитным свойствам вещества можно разделить на диамагнетики, парамагнетики и ферромагнетики.

В диамагнетиках атомы не обладают магнитным моментом. Но при включении магнитного поля электронные токи атомов, согласно правилу Ленца, пытаются ослабить внешнее магнитное поле. Этот эффект очень мал, магнитная восприимчивость χ отрицательна, около –10^-5 , магнитная проницаемость чуть меньше единицы. Диамагнитный эффект универсален, но в других веществах перекрывается более сильным парамагнитным или ферромагнитным эффектом.

В парамагнитных веществах атомы обладают магнитным моментом. При включении внешнего магнитного поля магнитные моменты атомов пытаются повернуться в направлении поля, но этому препятствует тепловое движение атомов. Магнитная восприимчивость мала, около +10^-3, магнитная проницаемость чуть больше единицы.