Электричество и электрическая железная дорога. Конспект лекций по физике, страница 38

Во-вторых, можно повысить напряжение контактной сети. Например, при повышении напряжения тяговой подстанции в два раза, сила тока уменьшится в два раза, а тепловые потери в четыре раза при постоянном сечении проводов. Поэтому существуют предложения повысить напряжение в контактной сети постоянного тока вместо 3 кВ до 6 кВ и даже до 12 кВ. По этой же причине применяется контактная сеть переменного тока с напряжением 25 и 50 кВ.

Определим  сопротивление контактного провода между ближайшими подстанциями при заданной мощности электровоза  Р.  Решая уравнение баланса мощности  относительно сопротивления контактного провода, получим

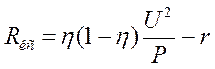.                                          (14.6)

По этой формуле при мощности двигателей  несколько МВт  величина сопротивления контактной сети должна  составлять  0,2–0,3 ом.  Тогда расстояние между подстанциями при площади сечении провода 200 мм² будет около 20 км.

4.   Ограничение силы тока по нагреву двигателей. В процессе работы электродвигатели нагреваются вследствие выделения теплоты на активном сопротивлении обмоток возбуждения и обмоток якоря и потерь на гистерезис при перемагничивании  железа якоря. Это может привести к перегреву двигателя. Теплота, выделяемая за некоторое малое время,  dQ= J²rdt , расходуется на теплоотдачу окружающей среде и нагрев двигателя.

Нагрев приводит к повышению температуры двигателя аккумулированной теплотой . Здесь m – масса двигателя, с – удельная теплоемкость материала (в основном это сталь), dT– повышение температуры. Теплоотдача окружающей среде пропорциональна площади теплоотдающей поверхности двигателя S и перепаду температур (Т-Т₀) между поверхностью двигателя и окружающей средой:  dQ_отд = α S (T–T₀) dt. Здесь α – коэффициент теплоотдачи, зависящий от способа теплоотдачи. Запишем уравнение теплового баланса

                                              14.7

Произведем расчет температуры двигателя в зависимости от времени работы. Пусть сила тока постоянна. Разделим в дифференциальном уравнении (14.7) переменные: время t и температуру T. В результате получим 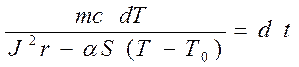. Проинтегрируем обе части уравнения в пределах: по времени от нуля до текущего момента t, по температуре от начальной Т₀ до текущей температуры Т 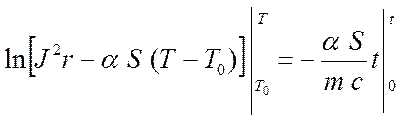 . Подставим пределы интегрирования и потенцируя, получим зависимость температуры корпуса двигателя от времени

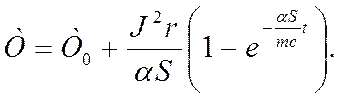     14.8

Температура корпуса растет со временем по экспоненциальному закону (рис.14.3). Скорость роста определяется коэффициентом показателя экспоненты 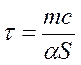. Это так называемое время релаксации. Чем больше масса и удельная теплоемкость двигателя, тем дольше по времени нарастает температура. В пределе, при бесконечно долгом времени работы температура стремится к равновесному значению. При этом температура корпуса становится предельной, а вся подводимая теплота рассеивается в пространство

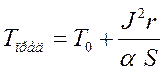.                                        14.9

Существует допустимая температура эксплуатации тяговых двигателей. Она ограничивает допустимое время работы двигателя. Чем выше сила тока, тем меньше допустимое время работы двигателя (рис. 14.3). Поэтому для увеличения длительности безопасной работы двигателя, чтобы доехать без остановки до следующей станции, приходится ограничивать силу потребляемого тока и мощность двигателей. Существует понятие «часовой режим» при котором в течении часа не допускается перегрева двигателей. По этому режиму определяется номинальная, паспортная мощность тяговых двигателей и допустимая сила тока.

Контрольные вопросы

1.  Как по графику (рис. 14.1) определить мощность тяговой подстанции, мощность двигателя и мощность тепловых потерь при заданном сопротивлении контактной сети и двигателей?

2. Как можно рассчитать сопротивление контактной сети?

3. Почему тяговые подстанции переменного тока располагаются на расстоянии друг от друга в три раза дальше, чем тяговые подстанции постоянного тока?

4. Почему электроэнергия от электростанций к потребителю передается под высоким напряжением в несколько сотен киловольт?