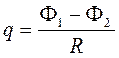Электричество и электрическая железная дорога. Конспект лекций по физике, страница 23

,                                                9.5

или для катушки

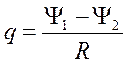 .                                             9.6

Формула используется для экспериментального измерения индукции магнитного поля. Пусть катушка площадью S с числом витков N помещается в исследуемую точку магнитного поля перпендикулярно силовым линиям. Катушка подсоединяется к прибору (веберметр), измеряющего количество электричества.  Потокосцепление катушки равно . Катушку выдергивают из магнитного поля, . Индукцию рассчитывают по формуле  .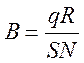

5.  Самоиндукция.

Если по контуру протекает электрический ток, то он создает магнитное поле, пронизывающее поверхность контура. При изменении силы тока происходит изменение  магнитного потока сквозь поверхность контура. По закону Фарадея возникает ЭДС электромагнитной индукции. Явление называется самоиндукцией.

Для проводников разной формы  с током индукция создаваемого магнитного поля, а значит и поток,  пропорциональны силе тока: . Для катушки потокосцепление пропорционально силе тока: . Коэффициент пропорциональности называется индуктивностью. Он характеризует способность проводников создавать магнитное поле.

По закону Фарадея ЭДС самоиндукции при постоянной индуктивности (когда отсутствуют ферромагнитные сердечники) определяется по формуле

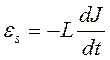.                                                 9.7

6. Выведем формулу индуктивности соленоида – катушки, длина которой много больше диаметра. Индукция магнитного поле в середине соленоида , где n– концентрация витков, то есть число витков на единицу длины, равное отношению числа витков к длине сердечника 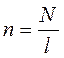.  При площади поперечного сечения сердечника Sпотокосцепление соленоида равно . Поделив на силу тока, введя объём сердечника , получим формулу индуктивности соленоида

.                                                9.8

7. Индуктивностью обладает любой элемент электрической цепи в зависимости от формы, размеров и магнитных свойств среды. Влияние явления самоиндукции следует учитывать для цепей с катушками трансформаторов, электрических двигателей. Можно пренебречь индуктивностью спиралей ламп накаливания, нагревателей, реостатов.

Явление самоиндукции в электрических цепях препятствует мгновенному как возрастанию тока при включении, так и спаду тока при отключении источника тока (рис.9.3).

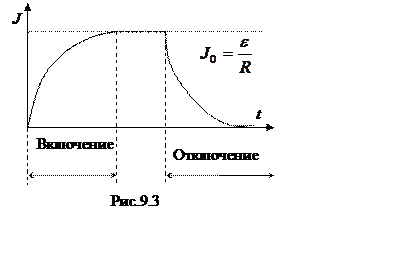 Например, в цепи из катушки индуктивностью L и резистором сопротивлением R от источника тока с ЭДС Eтечет установившийся ток силой 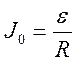. С помощью ключа катушка отключается от источника тока и замыкается на резистор. Ток постепенно спадает. В любой произвольный момент времени напряжения на резисторе равно ЭДС самоиндукции 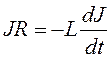 . Это дифференциальное уравнение первого порядка. Оно решается методом разделения переменных 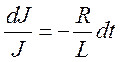. Интегрируя  с переменным верхним пределом 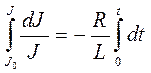 и потенцируя 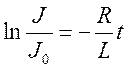 , получим зависимость силы тока от времени при отключении источника

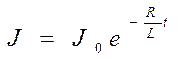.                                                9.9

Сила тока спадает по экспоненциальному закону.  За время, называемое временем релаксации 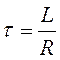,  сила тока уменьшается в   е=2,72 раза.  Чем больше индуктивность цепи, тем медленнее происходит спад тока.

Аналогично, решая задачу о включении цепи, получим зависимость

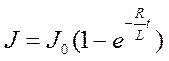 .                                                9.10

При отключении источника тока от цепи явление самоиндукции препятствует исчезновению тока. При большом сопротивлении зазора ключа R_ключ  падение напряжения на ключе в первое мгновение 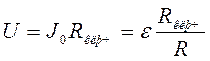 оказывается во много раз больше ЭДС источника. Происходит искровой пробой зазора ключа, образование дуги. Это приводит к разрушению контактов ключа.

На железной дороге с большими напряжениями и токами дуговой разряд является проблемой. Применяются различные способы гашения дуги: заполнение выключателя маслом, эле-газом,  отдувание дуги от контактов потоком воздуха или магнитным полем, деление дуги на части асбестовыми прокладками и т.д. Такие быстродействующие выключатели устанавливают на электровозах и подстанциях. При отключении сначала уменьшают силу тока. Например, при опускании токоприемника электровоза от контактной сети,  сначала вводят пусковой реостат.