 2. Закон Био-Савара-Лапласа. Экспериментальные
исследования магнитных полей проводников с током разных по форме привели к
неоднозначным результатам. Например, для прямого длинного проводника индукция
убывала обратно пропорционально расстоянию от проводника. Лаплас теоретически
установил закон для индукции магнитного поля, создаваемого малым элементом
проводника dl с силой тока J. В
скалярном виде в системе СИ он имеет вид
2. Закон Био-Савара-Лапласа. Экспериментальные
исследования магнитных полей проводников с током разных по форме привели к
неоднозначным результатам. Например, для прямого длинного проводника индукция
убывала обратно пропорционально расстоянию от проводника. Лаплас теоретически
установил закон для индукции магнитного поля, создаваемого малым элементом
проводника dl с силой тока J. В
скалярном виде в системе СИ он имеет вид
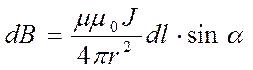 . 7.2
. 7.2
Здесь μ0 = 4π ∙10-7 Гн/м – магнитная постоянная, которая служит для установления соотношения между электрическими и механическими единицами в формуле, μ – относительная магнитная проницаемость, которая учитывает вклад в магнитное поле молекул среды. Для всех материалов кроме ферромагнетиков она незначительно отличается от единицы. Угол α между радиус-вектором r, проведенным из элемента проводника в точку наблюдения и вектором длины элемента.
Направление вектора индукции определяется правилом буравчика: если вворачивать буравчик в направлении тока, то вектор индукции направлен по вектору скорости конца ручки буравчика в точке наблюдения.
 3. Применение закона Био-Савара- Лапласа и принципа суперпозиции
для расчета магнитных полей проводников подтвердило результаты экспериментов. Например,
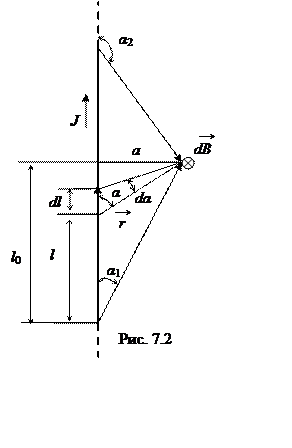
выведем формулу индукции магнитного поля отрезка прямого проводника с
током в точке на расстоянии а. от проводника (рис. 7.2). Выделим
элемент длиной dl на проводнике. Вектор индукции магнитного поля элемента,
а также всех других элементов, согласно правилу буравчика, направлен за чертеж.
По принципу суперпозиции
3. Применение закона Био-Савара- Лапласа и принципа суперпозиции
для расчета магнитных полей проводников подтвердило результаты экспериментов. Например,
выведем формулу индукции магнитного поля отрезка прямого проводника с
током в точке на расстоянии а. от проводника (рис. 7.2). Выделим
элемент длиной dl на проводнике. Вектор индукции магнитного поля элемента,
а также всех других элементов, согласно правилу буравчика, направлен за чертеж.
По принципу суперпозиции ![]()
![]() .
Подставим под знак интеграла формулу закона Био-Савара-Лапласа
.
Подставим под знак интеграла формулу закона Био-Савара-Лапласа ![]()
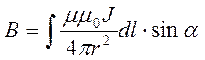 . Под знаком интеграла
три переменных. Перейдем к одной переменной – углу α по соотношениям
для сторон треугольника:
. Под знаком интеграла
три переменных. Перейдем к одной переменной – углу α по соотношениям
для сторон треугольника: ![]()
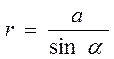 ,
,
![]() , откуда после дифференцирования
, откуда после дифференцирования
![]()
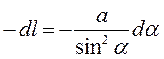 . Подставим полученные
соотношения между переменными
. Подставим полученные
соотношения между переменными 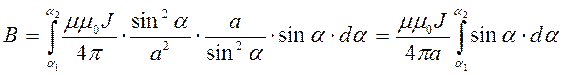 и после сокращения
проинтегрируем. Получим формулу индукции магнитного поля отрезка прямого проводника
и после сокращения
проинтегрируем. Получим формулу индукции магнитного поля отрезка прямого проводника
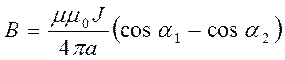 7.3
7.3
Если проводник бесконечно длинный (a << l, α1→0, α→π ), то формула для индукции принимает вид
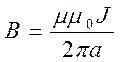 . 7.4
. 7.4
Как и в опытах Био и Савара индукция магнитного поля убывает обратно пропорционально расстоянию от проводника, а силовые линии поля являются концентрическими окружностями.
 4. Силовые векторные поля характеризуют циркуляцией
вектора по некоторому контуру и потоком вектора через поверхность контура. Поток
по определению равен интегралу от скалярного произведения вектора индукции по
площади контура:
4. Силовые векторные поля характеризуют циркуляцией
вектора по некоторому контуру и потоком вектора через поверхность контура. Поток
по определению равен интегралу от скалярного произведения вектора индукции по
площади контура: 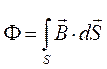 . Поток пропорционален числу
силовых линий, пронизывающих контур.
. Поток пропорционален числу
силовых линий, пронизывающих контур.
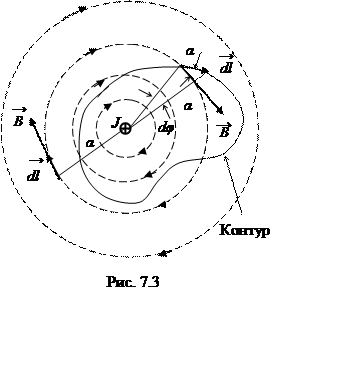
Определим циркуляцию вектора индукции 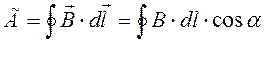 для уже известного магнитного поля длинного
проводника с током по некоторому контуру, охватывающем проводник. (рис.7.3). Произведение
для уже известного магнитного поля длинного
проводника с током по некоторому контуру, охватывающем проводник. (рис.7.3). Произведение
![]() – это проекция вектора элемента длины на
вектор индукции, которая равна длине дуги
– это проекция вектора элемента длины на
вектор индукции, которая равна длине дуги ![]() .
Подставив формулу индукции поля длинного проводника с током, получим
.
Подставив формулу индукции поля длинного проводника с током, получим 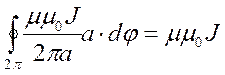 . Циркуляция вектора индукции не зависит от
формы контура интегрирования, ни от его размеров, ни от положения проводника
внутри контура. Обобщим на произвольное число проводников с током:
. Циркуляция вектора индукции не зависит от
формы контура интегрирования, ни от его размеров, ни от положения проводника
внутри контура. Обобщим на произвольное число проводников с током:
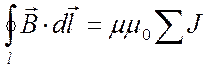 . 7.5
. 7.5
Это закон полного тока: циркуляция вектора индукции магнитного поля по произвольному контуру равна произведению абсолютной магнитной проницаемости среды на алгебраическую сумму токов, пронизывающих поверхность, ограниченную контуром интегрирования.
5. Закон полного тока позволяет в задачах с известным
распределением магнитного поля сравнительно легко определить индукцию.
Рассмотрим пример, поле тороида – катушки, намотанной равномерно на тор. Пусть
тор имеет разрез, воздушный зазор (рис. 7.4). Силовые линии магнитного поля
это окружности. Индукция магнитного поля вдоль окружности одинакова как в сердечнике,
так и в воздушном зазоре. Это связано с тем, что силовые магнитного поля
замкнуты, а при малой длине зазора их густота и индукция почти неизменна. Если
длины сердечника и зазора равны lиl0 , магнитные проницаемости μμ0 и μ0
то сумма токов, пронизывающих поверхность внутри окружности равна произведению
числа витков на силу тока. Интеграл по замкнутому контуру представим суммой
двух интегралов по контуру в сердечнике и зазоре. Таким образом, по закону
полного тока 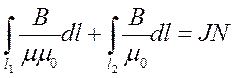 . Индукция магнитного поля в
сердечнике тороида одинакова по силовой линии и равна
. Индукция магнитного поля в
сердечнике тороида одинакова по силовой линии и равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.