Электричество и электрическая железная дорога. Конспект лекций по физике, страница 25

10. ВЗАИМНАЯ ИНДУКЦИЯ

1. Пусть рядом расположены два магнитосвязанных контура, так что их магнитные поля пронзают поверхности друг друга. Если в одном из контуров изменяется сила тока, то поток магнитной индукции сквозь поверхность второго контура также изменяется. Согласно закону Фарадея во втором контуре возникает  ЭДС электромагнитной индукции, индукционный ток.  В этом заключается явление взаимной индукции.

Очевидно, что поток вектора магнитной индукции сквозь поверхность второго контура пропорционален силе тока в первом контуре    и наоборот, поток сквозь поверхность первого контура пропорционален силе тока во втором контуре  . Если рядом расположены катушки, то потокосцепления сквозь витки катушек также пропорциональны силам тока в соседних катушкках:   и .  Коэффициенты пропорциональности L₁₂ и L₂₁ называются коэффициентами взаимной индукции.

Закон Фарадея для явления взаимной индукции при постоянном значении коэффициента взаимной индукции принимает вид

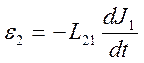,      и 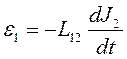   .                                       10.1

По правилу Ленца  индукционный ток в катушке течет так, чтобы поддержать, не дать измениться величине силы тока в другой катушке, создающей магнитное поле.

2. Выведем формулу коэффициента взаимной индукции двух соленоидов на общем сердечнике.  Пусть по первой катушке с концентрацией витков n₁протекает ток J₁, и она является источником магнитного поля с индукцией в общем сердечнике  .  Потокосцепление сквозь витки второй катушки равно . Подставив индукцию магнитного поля, заменив число витков через концентрацию витков , и введя объем сердечника , в итоге получим .  Сопоставив с формулой потокосцепления , получим для коэффициента взаимной индуктивности двух соленоидов формулу

.                                                            10.2

Если считать источником магнитного поля вторую катушку, то получили бы точно такую же формулу. То есть коэффициенты взаимной индукции обеих катушек одинаковы .

3. Запишем закон Ома для двух магнитосвязанных контуров. Пусть первый контур подключен к источнику тока с ЭДС ε.  Согласно второму правилу Кирхгофа падение напряжения в первом контуре равно алгебраической сумме  ЭДС: источника тока, ЭДС самоиндукции и ЭДС взаимной индукции из-за появления тока во втором контуре:

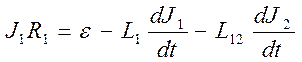.                                     10.3

Во втором контуре падение напряжения на активном сопротивлении провода равно алгебраической сумме ЭДС взаимной индукции, обусловленной изменяющимся током в первом контуре и ЭДС самоиндукции второго контура:

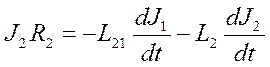.                       10.4

Чтобы определить токи в контурах следует совместно решить совместно систему дифференциальных уравнений закона Ома.

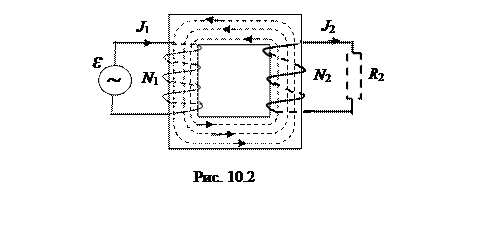
4. Трансформатор – это статическое устройство, основанное на явлении взаимной индукции, предназначенное для изменения напряжения и силы тока в цепях переменного тока. 

На  замкнутом ферромагнитном сердечнике расположены катушки. В простейшем случае их две: первичная, подключенная к генератору переменного напряжения и вторичная, замкнутая на нагрузку (рис.10.2). Чтобы при заданной ЭДС генератора и параметров катушек определить токи и напряжения, следует решить уравнения закона Ома 10.3 и 10.4 для двух магнитосвязанных катушек. Рассмотрим простейший случай – режим холостого хода трансформатора, когда нагрузка во вторичной цепи отсутствует: R₂→∞,  J₂→0. Но произведение  равно напряжению на выводах вторичной катушки. По уравнению 10.4 напряжение U₂  равно ЭДС взаимной индукции: 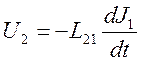.  Сопротивление катушек при изготовлении делается по возможности меньше. Поэтому падением напряжения в первичной катушке в уравнении 10.3   по сравнению с ЭДС генератора можно пренебречь 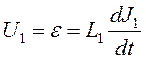.  Сопоставляя напряжения на выводах катушек, получим 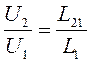. Подставив формулы для коэффициентов взаимной индукции и самоиндукции первой катушки, получим, что отношение напряжений на выводах катушек пропорционально отношению чисел витков катушек:

.                                                    10.5