2. Показана эффективность метода в смысле уменьшения суммарных затрат по сравнению с полным контролем и целесообразность его использования в автоматизированных системах технологического контроля.
В дополнение к изложенному подходу по использованию статистических связей между параметрами объекта контроля (ОК) ниже рассмотрен информационный критерий выбора системы параметра ОК, позволяющий с более общих позиций теории информации подойти к решению данной задачи. Примером такого подхода является [7].
2.3.2 Обобщённая модель измерений
Измеренная величина представляется следующей моделью:
Z(t) = [ξ(t) + 1]Uс(t) + Δc(t) + Y(t), (1)
где ξ(t) – мультипликативная случайная погрешность, Uc(t) - истинное значение измеряемого сигнала, Y(t) - аддитивная случайная погрешность, в общем случае зависящие от времени и распределённые с плотностями вероятности f(ξ), f(uc) и f(y) соответственно; Δc(t) – систематическая погрешность.
Суммарная функция затрат имеет вид:
,
(2)
где KU - коэффициент затрат на измерение; Kα и Kβ - коэффициенты затрат на потери из-за ошибок α и β; αср(σ) - средняя вероятность ошибки I-ого рода; βср(σ) - средняя вероятность ошибки II-ого рода.
Определяем ошибки первого и второго рода с использованием ненормированных функций распределения показателя, которые разделены на три группы [4]:
ψ1(u) - для первой части объектов контроля (ОК), у которых показатель качества признан ниже области допустимых значений;
ψ2(u) - для принятой части ОК;
ψ3(u) - для третьей части ОК, у которых показатель качества признан выше области допустимых значений.
Эти распределения определяются следующими выражениями:
,
(3)
,
(4)
.
(5)
В этих выражениях f(u) и f(z) – плотности вероятностей измеряемого параметра u и аддитивной измерения z соответственно.
При этом вероятности ошибок первого и второго рода (α и β) определяются по следующим формулам:
,
(6)
.
(7)
Результат i-го измерения имеет вид
zi = [ξi + 1]Uсi + Δci + yi = Uсi + [ξiUсi + (Δci + yi)].
Плотность распределения суммы систематической и аддитивной погрешностей:
f(y + Δc) =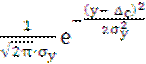 
=
dnorm(y, Δc,
σy), где
Δc – математическое ожидание; σy –
среднеквадратическое отклонение величины y.
Примечание.- Здесь и ниже dnorm(x,µ,σ) – гауссова плотность вероятности в обозначениях MathCAD.
Плотность распределения мультипликативной погрешности:
f(ξ) = dnorm(ξ,0, σξ).
Плотность распределения f(ξUс):
f(ξUс) =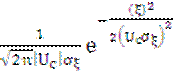 
= dnorm(ξ, 0,
Uc·σξ).
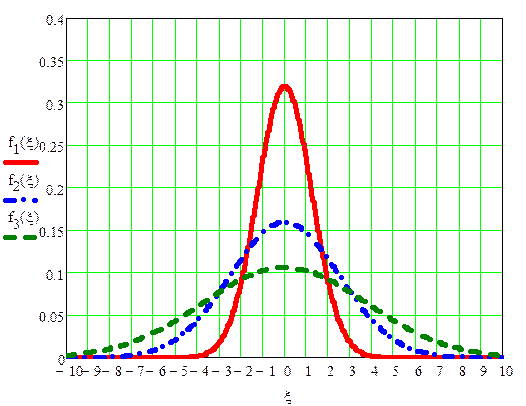
Рис. 1.
На рис.1 изображены распределения f(ξUс) при Uc1 = Uн = 5, Uc2 = Uном = 10, Uc3 = Uв = 15.
Распределение величины Z является нормальным, т. к. Z является суммой двух случайных величин, имеющих нормальное распределение.
Тогда
f(z) = 
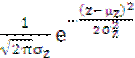, где
μz = Uc + Δc; σz =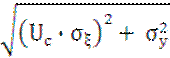 
.
f(z) = dnorm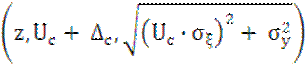
.
На рис.2 слева направо показаны распределения f1(z), f2(z), f3(z), f4(z), f5(z) при значениях Uc = 3; 5; 10; 15; 17.
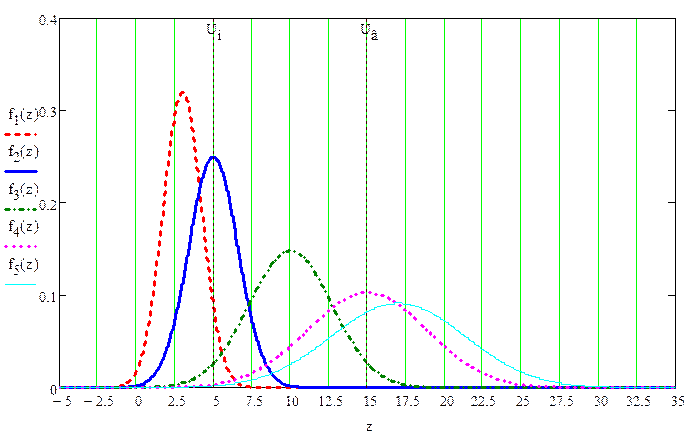
Рис. 2.
Ошибка первого рода (риск поставщика):
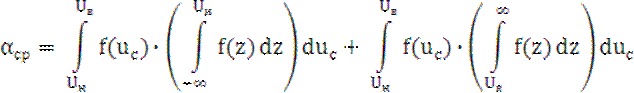
где Uн, Uв – границы поля допуска измеряемого параметра.
Тогда
.
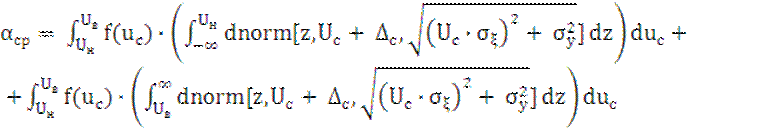Рассмотрим зависимости ошибки первого рода от СКО мультипликативной и аддитивной погрешностей.
На рис. 3 представлен график зависимости αср(σy) при σy = 1,2…20 для различных значений σξ. Учитывая, что σξ<< Uc, возьмём σξ1 = 0; σξ2 = 0.25; σξ3 = 0.5; σξ4 = 0.75; σξ5 = 1.
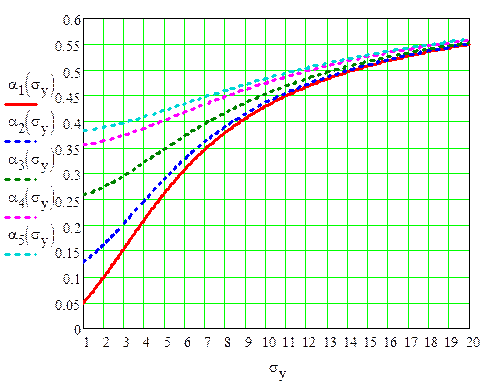
Рис.3. Зависимость ошибки первого рода от СКО аддитивной погрешности измерения
График построен при следующих значениях: μu = Uном = 0, σu = 5;Uв = 5, Uн = -5; Δс = 0.5.
Ошибка второго рода (риск заказчика):
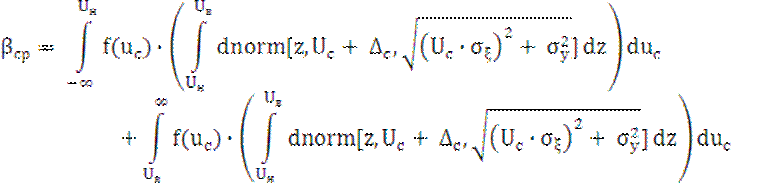
Зависимость βср(σy) изображена на рис. 4 при тех же значениях.
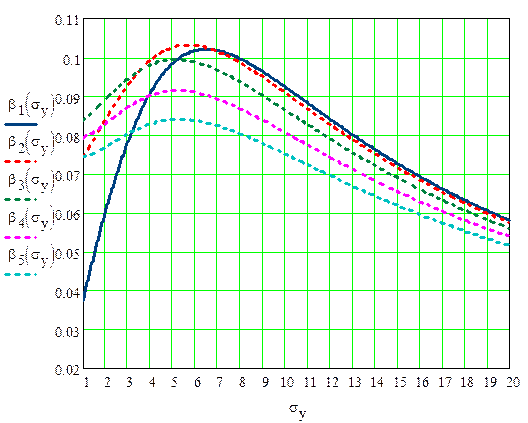
Рис. 4. Зависимость ошибки второго рода от СКО аддитивной погрешности измерения
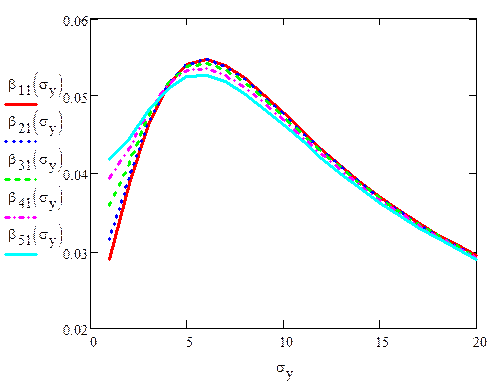
Рис.5 β’(σy)
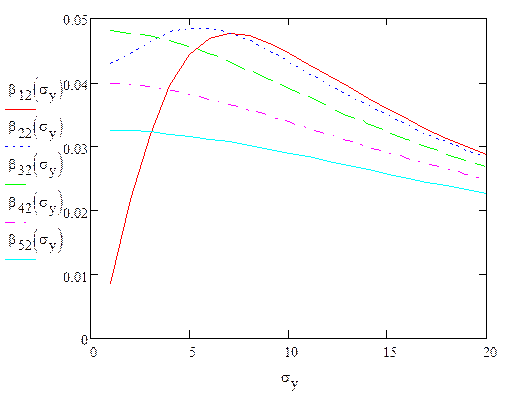
Рис.6 β’’(σy)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.