Качество и эффективность метрологического обеспечения, страница 23

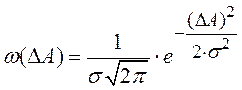
где ΔА= Х - А; ΔА - случайная погрешность; Xи А - соответственно измеренное и истинное (при нулевой систематической составляющей погрешности) значения измеряемой величины;

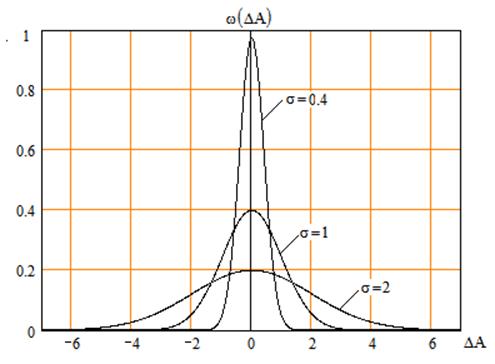
σ - среднеквадратическое отклонение. Чем больше  величина параметра σ, тем больше разброс результатов измерений относительно среднего значения (рисунок), тем ниже точность измерения. На практике обычно считают, что погрешность измерения по модулю не превышает 3σ, так как вероятность этого события:

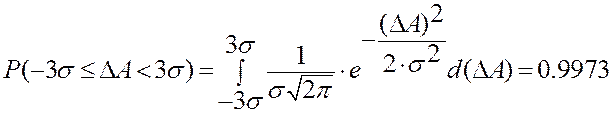                            (7)

близка к единице. Величину Δ_max=3σ  называют предельной абсолютной погрешностью, а 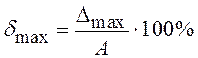 -  предельной относительной погрешностью. Используя соотношение (7), можно утверждать, что с вероятностью Р = 0,9973 истинное значение измеряемой величины лежит в интервале   Х± Δ_max. В более общем стучав пользуются понятием доверительного интервала, под ним понимается интервал, который с заданной доверительной вероятностью  содержит искомое значение оцениваемого параметра А , т.е.

где - доверительный интервал;  и - доверительные границы Величину α называют уровнем значимости и выбирают в пределах 0,001 - 0,01.

На примере нормального распределения покажем, как отыскиваются доверительные границы. Величина

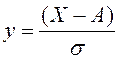 имеет нормальное распределение  с нулевым средним и единичной дисперсией, т.е. плотность вероятности задается выражением

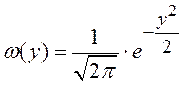
В случае симметричных границ  a₁ = a₂ = a, и

,

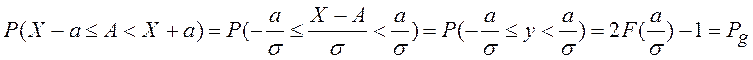где 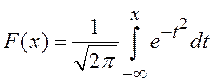- интеграл Лапласа.  Отсюда  ,

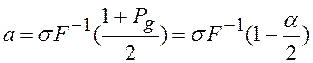где  - функция, обратная к , - доверительная вероятность. Функция  подробно табулирована (см. прил. 1), поэтому, зная 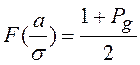 легко найти α. Например =0,9973, 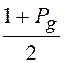=0,99865 и из таблицы прил. 1 находим =3; a=3σ.

Для того, чтобы минимизировать систематическую и случайную погрешности, используют обработку результатов измерении. Влияние систематической составляющей уменьшается анализом уравнения измерения, выбором надлежащей методики измерений и расчетом соответствующих поправок. Эта задача решается на этапе проектирования средств измерений и в настоящей работе не рассматривается. Поэтому в дальнейшем анализируются методы обработки результатов намерений, позволяющие уменьшить влияние случайных погрешностей.

Поскольку закономерности случайных величин проявляется лишь при их многократном появлении, то уменьшение случайных погрешностей достигается путем проведения многократных измерений и соответствующей обработкой результатов. Возможны несколько постановок задачи обработки. Сформулируем их.

Пусть в результате проведения n независимых прямых измерений величины А получены значения x₁,x₂…x_n, которые содержат случайные погрешности Δ₁,Δ₂…Δ_n, т.е.

x_i=A+ Δ_i,    1 ≤ i ≤ n.                                                                       (8)

Первая задача обработки состоит в отыскании оценки величины А (обозначим ее), обладающая свойствами:

1)  Оценка должна быть несмещенной, т.е. ее среднее значение должно совпадать с истинным значением измеряемой величины. Это требование обуславливает отсутствие систематических погрешностей в результате обработки

2)  Дисперсия оценки  должна быть минимальной. Это требование обеспечивает минимальное влияние случайной погрешности на конечный результат измерений.

Вторая задача обработки результатов измерений состоит в определении дисперсии случайной погрешности однократного измерения, третья задача сводится к исключению грубых погрешностей (промахов). Рассмотрим несколько вариантов первой задачи.

1.1Прямые равнорассеянные измерения, случай известной дисперсии

Равнорассеянными измерениями называются такие измерения, для которых справедливо равенство:

При многократных эталонных измерениях мер на одной и той же аппаратуре можно определить с высокой точностью значение  и считать его известным. Вид функции (8) показывает, что оценку  можно искать в виде линейной функции результатов измерений .

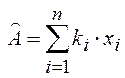, где  - некоторые коэффициенты.

Исходя из условий 1) и 2) имеем:

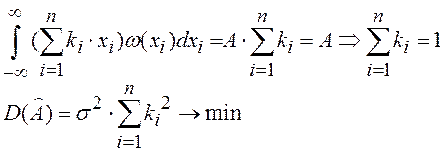                                            (9)