Качество и эффективность метрологического обеспечения, страница 18

С точки зрения теории информации ТП можно рассматривать как некоторый случайный объект с конечным числом состояний {C_j}, j = l,m с соответствующими вероятностями p(C_j).

Действительно, если выбранная размерность вектора параметров  удовлетворяет наперед заданным требованиям, то число состояний ТП

т = 2ⁿ                                                                               (1)

так как каждая из n составляющих вектора Y_n может принимать одно из двух состояний: принадлежности либо не принадлежности допуску  [y_iн, y_iв ] с соответствующими вероятностями

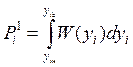                                                                    (2)

                                                                           (3)

Здесь , i=l,n - закон распределения вероятностей. Неопределенность состояния ТП определяется значением энтропии [2, 3]

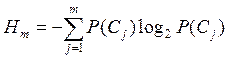                                                    (4)

где - вероятность j - го состояния ТП, вычисляемая известными способами [4,5] с использованием значений вероятностей , .

Для случая статистической независимости составляющих вектора Y_n вероятность состояний, имеющих k дефектных параметров, определяется выражением [4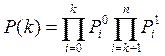,5]

                                                               (5)

где k - число параметров из n, не вошедших в поле допуска.

При k = 0 вероятность состояний

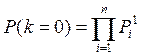                                                                             (6)

соответствует вероятности попадания в допуск всех параметров ТП, т.е. вероятности работоспособного состояния.

способного состояния.

При k=nимеем другую крайнюю ситуацию, когда ни один параметр ТП не принадлежит полю допуска с вероятностью

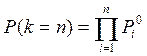                                                                               (7)

При условии равновероятностного распределения состояний

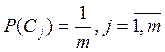                                                              (8)

значение энтропии (4) максимально и равно числу параметров ТП

H_{m max} = - log₂2ⁿ =n(9)

Энтропия минимальна и равна нулю Н_т=0, если вероятности какого-либо состояния =1, а вероятности остальных равны нулю, как, например, в крайних случаях (6) и (7). Это справедливо и в промежуточных ситуациях, когда k параметров с вероятностью =1,   , k не входят, а n-k с вероятностью =1, входят в поле допуска.

Рассмотренные свойства энтропии (4) и вероятности состояний (5) позволяют сформулировать следующие утверждения:

- энтропия (4) максимальна и равна значению (9) при

=                                                                    (10)

Вероятности состояний равны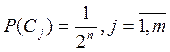

- при ≠распределение вероятностей состояний отличается от равновероятностного и при >минимум энтропии (4) соответствует максиму вероятности (6) нахождения параметров ТП в поле допуска.

- при < ≤ 1 значения энтропии заключены в пределах 0 ≤ Н_т ≤ п, Н_т → 0 при → 1. Таким образом, минимум энтропии   имеет место только при выполнении условия 0,5<≤1

Рассмотренные выше свойства энтропии n - мерного ТП позволяют сформулировать критерий оценки его состояния, заключающийся в том, что, если значения энтропии Н_m  ТП не превышает некоторое допустимое значение максимального (порогового) значения Н^*, т.е.

0≤ Н_m≤ Н^*                                                                         (11)

и если при этом 0,5<≤1, то ТП считается неразлаженным и регулированию не подлежит.

При невыполнении условия (11) принимается решение о регулировании ТП.

Пороговое значение энтропии находится по заданной вероятности работоспособного состояния ТП, определяемого выражением (6)

H^* = -{P(k = 0)1оg₂Р(k=0)+[1 - Р(k = 0)]log₂[1 - Р(k = 0)]}      (12)

Уравнение (12) предполагает брак, если хотя бы один параметр ТП не в поле допуска с вероятностью 1 – Р(k= 0) .

Предлагаемый критерий можно обобщить на случай статистически зависимых параметров ТП. Энтропия n-мерного ТП Н_т удовлетворяет условию [2,3]

<Н_т(13)

где Н_m находится по формуле (4).

В многооперационных ТП, содержащих ℓ операций технологического контроля, оценку состояний ТП можно производить на каждой контрольной операции по критерию (11). Для этого достаточно знать число  контролируемых параметров на каждой операции и нормы на вероятность выхода годных изделий для определения порогового значения Н^*, энтропии (12).