Качество и эффективность метрологического обеспечения, страница 21

Вывод дисперсии оценки (4.25) выполняется по аналогии с (4.31).

Информативность предлагаемого дискретного подхода хорошо просматривается на примере оценки (4.31). Это прежде всего относится к характеру влияния априорной информации о параметре а.

Из выражений (4.31) видно, не только как формируется оценка , но и то, как относительный разброс априорных данных  влияет на объём выборочных данных

1.  Генерация случайных чисел (времён отказа). Для обработки алгоритмов (4.28) и (4.29) оценки  необходимо разработать генераторы (датчики) законов распределения ВБР.

Здесь остановимся на генерации распределений Вейбулла и трёхэкспоненциального распределения.

Исходным является датчик равномерно распределённых случайных чисел в интервале .

При известной функции преобразования

,                                                                                            (4.33)

где  - времена, соответствующие j-му моменту отказа. Плотность вероятности определяется по стандартному правилу

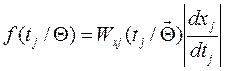                                                                       (4.34)

Для распределения Вейбулла функция преобразования (4.33) имеет вид

                                                                                   (4.35)

Тогда в соответствии с (4.34) получим распределение Вейбулла (усечённое сверху):

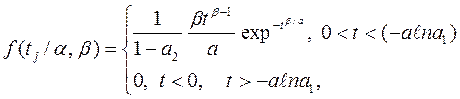                                (4.36)

здесь а и  - коэффициенты масштаба и формы соответственно.

При  распределение (4.36) переходит в усечённое экспоненциальное

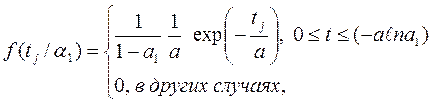                                    (4.37)

здесь , где  - интенсивность отказов, 1/ч. 

Трёхэкспоненциальное распределение ВБР [3, 5]:

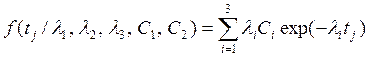,                                              (4.38)

где  - весовые коэффициенты, имеющие смысл вероятности с условием нормировки .

Распределение (4.38) является композиционным, поэтому алгоритм генерации случайных чисел [] более сложен:

1) формируются три независимых датчика случайных чисел, распределённых по экспоненциальному закону с интенсивностями  в соответствии с функцией преобразования (4.35) при =1.

Полученные три массива случайных чисел записывают в ОЗУ;

2) весовые коэффициенты  формируются с использованием датчика равномерно распределённых в [,] чисел, методом разбиения интервала [,] на части, пропорциональные   и  попадания случайного числа [] в соответствующую часть интервала [,];

3) сформированный по п. 2 массив случайных чисел [] с распределением (4.38) записывается в ОЗУ2. Данный массив [] может использоваться для получения оценок вектора параметров в соответствии с (4.28), (4.29), либо поступать в блок статистической обработки для получения гистограммы и проверки на критерий согласия.

Приложение 1

1.  Измерения и обработка результатов измерений

Измерения играют важную роль в науке и технике, С их помощью получают количественные оценки изучаемых особенностей объектов или явлений. Под измерением в метрологии понимают- совокупность экспериментальных и вычислительных операций по определению количественных соотношений между измеряемой величиной и единицей ее измерения и оценки погрешности результата измерений. Математическая сущность процесса измерения может быть представлена выражением

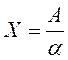
где X - числовое значение измеряемой величины А, показывающее во сколько раз она больше или меньше единицы измерения α

Процесс измерения представляет собой физический эксперимент, в результате которого устанавливается соотношение между измеряемой величиной и единицей измерения. Значение величины, которое идеальным образом отражало бы в качественном и количественном соотношениях существующее свойство объекта, называется истинным значением. В зависимости от способа получения результата, измерения делятся на прямые и косвенные.

Прямыми называются измерения, результат которых получается непосредственно из опытных данных,, Примеры прямых измерений: измерение диаметра детали микрометром, тока - амперметром, температуры - термометром.

Косвенными называются измерения, При которых искомая величина непосредственно не измеряется, а ее значение находится на основании известной зависимости между этой величиной и величинами, полученными в результате прямых измерений. В настоящей работе используются только прямые измерения.