Значения Н* на каждой операции должны удовлетворять условию
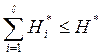(14)
где Н* - пороговое значение (12) энтропии всего ТП. Знак равенства в соотношении (14) выполняется при статистически независимых операциях (участках ТП, охватываемых операциями контроля), когда вероятность годного изделия на выходе ТП равна (6) при п=ℓ.
Условие (14) позволяет перераспределять уровни пороговой энтропии (или точности изготовления) между участками ТП.
Произведенный анализ ТП как дискретного источника сообщений с конечным числом сообщений с конечным числом состояний, вероятности (5) которых зависят от вероятностей годности (2) и брака (3) по каждому параметру, доказывает принципиальную возможность использования информационного критерия (11) для оценки состояния ТП при условии достаточности статистики при оценке вероятностей (2) и (3).
Изменения исходных вероятностей (2) и (3), а, следовательно, и вероятностей состояния (5) могут происходить как из-за изменения средних значений (разладка ТП), так и за счет изменения среднеквадратических отклонений параметров (погрешностей ТП).
Эффективность информационного критерия (11) можно повысить, используя независимость дифференциальной энтропии (ε - энтропии) [2,3] от математического ожидания. Для многомерного ТП (либо участка ТП, охваченного контролем) ε - энтропия равна
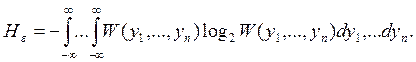(15)
Верхняя оценка ε - энтропии (15) определяется выражением [2,3].
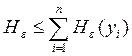, (16)
где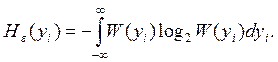 
Знак равенства в выражении (16) соответствует статистической независимости составляющих вектора Yn. При отсутствии данных о законах распределения можно воспользоваться принципом максимума ε - энтропии гауссовского распределения [2,3] и использовать верхнюю границу оценки для значений энтропии (15).
Таким образом, можно
дополнить критерий (1) проверкой изменения ε -
энтропии, с целью установления причины его нарушения: если условие
(11) не выполняется, a 
=const для t
[t1, t2], то
причиной тому является разладка ТП (уход средних). В противном случае произошли
и разладка и ухудшение точности (среднеквадратических отклонений параметров) ТП.
Рассмотрим влияние достоверности контроля на оценку состояния ТП. Минимальный уровень неопределенности оценки состояния ТП определяется как погрешностями контроля (аппаратурными и методическими), так и за счет ограниченности объемов выборок при оценке статистических характеристик.
Максимальный допустимый уровень неопределенности, вносимый любой операцией контроля, может быть определен в соответствии с формулой (4) как
Hki = -(Pni log2Pni+P0i log2P0i ) (17)
где Pni, P0i =1 - Pni - вероятности правильной и ошибочной оценки значений параметров (или хотя бы одного параметра) ТП.
В свою очередь вероятность ошибки при нормальном контроле равна P0i =α+β,(18)
где α, β - вероятности ошибки I и II рода [6].
При наличии ℓ контрольных операций в ТП максимальная энтропия, вносимая контролем, равна
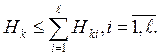(19)
Знак равенства в выражениях (19) соответствует статистической независимости контрольных операций.
Остаточная энтропия равна:
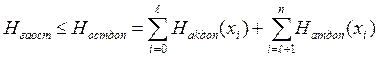, (20)
где первая сумма определятся допустимым уровнем ошибок I и II рода (4) (αдоп , βдоп соответственно) при контроле 0 ≤ ℓ ≤ n параметров; вторая сумма - допустимым значениям вероятности брака за счет неконтролируемых (n-ℓ) параметров.
При этом всегда должно удовлетворяться условие H*max ≥0. Уравнение (20) показывает, что точность изготовления и точность контроля можно перераспределять между собой, но при условиях, что неопределенность ТП с учетом контроля не превышает заданный пороговый уровень Н* , определяемый выражением (12). Можно показать, что данный подход может быть распространен и на задачу выбора контролируемый параметров [7].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.