Принципиальным для практического использования информационного подхода, изложенного выше, является следующее.
1. Информационный критерий оценки состояния ТП позволяет использовать данные о вероятности выхода годных (брака) изделий для регулировки ТП в целом и его частей, охваченных контролем.
2. Возможности перераспределения допустимой энтропии (12) позволяют решить задачи назначения предельных точностей обработки на каждой технологической операции, что весьма важно на этапе технологической подготовки производства.
3. Анализ влияния контроля на оценку энтропии ТП позволяет поставить задачу расстановки контрольных операций и назначения их точности (достоверности), обеспечивающей минимум энтропии (17) контроля, определяемый заданными требованиями на вероятности ошибок I и II рода.
4. Задание максимально допустимого уровня неопределенности ТП, задаваемого пороговым значением энтропии (12), позволяет оценить объемы (количество) информации, требующейся для переработки в системах контроля, что весьма важно для определения требований к этим системам при автоматизированном контроле.
4.Накопление информации в автоматизированных системах ИЗМЕРЕНИЙ
Как уже отмечалось выше, автоматизированные системы измерительного контроля позволяют накапливать информацию о надежности продукции или услуги связи. Накопленные данные являются априорной информацией (при соответствующей обработке) для оценок параметров распределения вероятности безотказной работы в процессе производства и для прогнозирования эксплуатационной надежности.
В данном примере рассмотрен метод байесовских оценок параметров закона распределения отказов при условии конечного числа априорных данных о параметрах распределения, т.е. когда априорное распределение имеет дискретный характер.
Достоинством байесовского подхода к оценкам распределения вероятности безотказной работы (ВБР) является более высокая точность по сравнению с другими методами и возможность использования априорной информации [7] . Указанные свойства являются весьма важными в процессе управления надежностью производства продукции и услуг связи, а также в ряде метрологических задач при использовании автоматизированных систем измерительного контроля с элементами адаптации. Эта задача в принципе имеет классический характер, прежде всего, для непрерывных распределений ВБР и априорных распределений вектора параметров.
В настоящей работе мы поставили перед собой цель подробнее рассмотреть данный вопрос в приложении к задачам оценки параметров ВБР при дискретном характере априорных распределений вектора параметров для различных законов. Приведены методы генерации этих распределений ВБР.
1. Байесовские оценки вектора параметров распределения ВБР. При
известно модели ![]() байесовская оценка среднего и
дисперсии АПВ вектора параметров для квадратичной функции потерь имеют вид:
байесовская оценка среднего и
дисперсии АПВ вектора параметров для квадратичной функции потерь имеют вид:
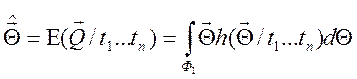 , (4.24)
, (4.24)
где
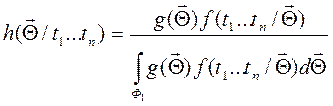 (4.25)
(4.25)
апостериорная ПВ вектора; ![]() - априорная ПВ;
- априорная ПВ; ![]() - область интегрирования;
- область интегрирования; ![]() – размерность вектора
– размерность вектора ![]() ,
, ![]() = 1, m.
= 1, m.
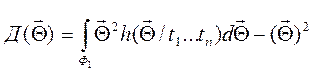 . (4.26)
. (4.26)
При дискретном виде априорной ПВ вектора ![]()
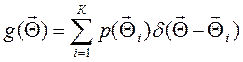 , (4.27)
, (4.27)
где К – число дискрет распределения.
Оценки (4.24) и (4.25) с учётом
(4.26) и (4.27) при статически независимых составляющих вектора ![]() и отсчетов
и отсчетов ![]() имеют вид
имеют вид
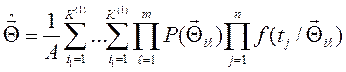 , (4.28)
, (4.28)
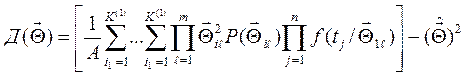 . (4.29)
. (4.29)
В выражениях (4.28) и (4.29)
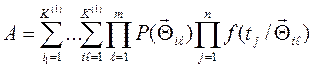 . (4.30)
. (4.30)
Порядок
суммирования в (4.28)… (4.29), как интегрирования в (4.24) и (4.26) зависят от
последовательности определений i-й
составляющей вектора ![]() .
.
В
качестве примера дискретного подхода рассмотрим случай вейбулловской модели при
известных коэффициентах формы ![]() . В этом случае оценка
(4.28) коэффициента масштаба
. В этом случае оценка
(4.28) коэффициента масштаба ![]() имеет вид
имеет вид
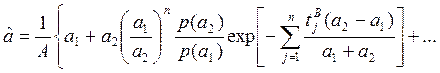
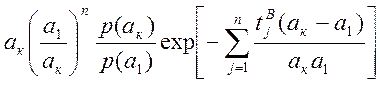 , (4.31)
, (4.31)
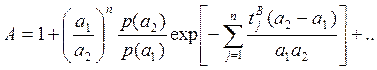
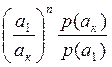
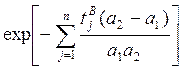 (4.32)
(4.32)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.