Качество и эффективность метрологического обеспечения, страница 24

Следовательно, задача нахождения оценки  сводится к нахождению таких значений k₁,k₂…k_n, при которых выполняются условия (9). Можно показать, что условиям (9) удовлетворяет решение

k₁=k₂=k_n=1/n

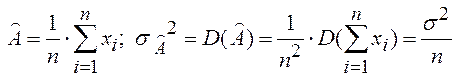
Из последней формулы следует, что среднеквадратическая погрешность  результата измерений в  раз меньше среднеквадратической погрешности отдельного измерения . Соответственно доверительный интервал на уровне значимости α, результата обработки:

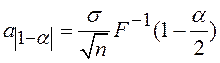                                                              (10)

Прямые равнорассеянные измерения, случай неизвестной дисперсии

Если дисперсия  величины x_i неизвестна, то в качестве оценки величины А по-прежнему принимают величину:

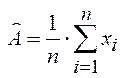                                                                      (11)

Однако доверительный интервал при этом уже нельзя определять из выражения (10). В этом случае поступают следующим образом: известно, что если x₁,x₂…x_n распределены по нормальному закону, то величина

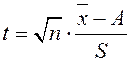                                                                     (12)

распределена по закону Стьюдента с (n-1)-ой степенью свободы, плотность вероятности которого:

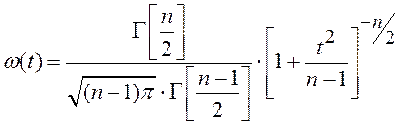                                             (13)

в (12) и (13) ; ; 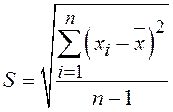 - гамма функция. Величину S² называют выборочной дисперсией совокупности величин x₁,x₂…x_n.

Доверительный интервал  оценки  найдем из уравнения:

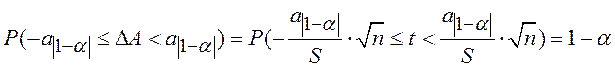                             (14)

где α – уровень значимости. Из выражения (14) находим:

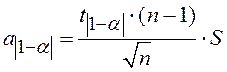
где - коэффициент Стьюдента, зависящий от уровня значимости α и числа степеней свободы (n-1) и определяемый из таблицы 1.

При n≥30 распределение Стьюдента практически совпадает с нормальным, дисперсия которого:

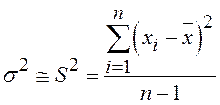                                                             (15)

Для расчета доверительных границ в этом случае можно воспользоваться выражением (10).

Таким образом, нами попутно решена вторая задача обработки результатов измерений – определение дисперсии случайной погрешности однократного измерения. Значение дисперсии задается выражением (15).

Рассмотрим решение третьей задачи обработки результатов измерений – исключение грубых погрешностей. Грубые погрешности (промахи) вызываются неправильным использованием средств измерений, неправильными отсчетами по шкале прибора, ошибками в вычислениях и недостатком опыта оператора. Для устранения промахов из протоколов измерений применяют различные критерии грубых погрешностей. Один из них – отклонение от среднего на уровне значимости α. При α=0,27% и при известной дисперсии однократного измерения  результат измерения X_j признают содержащим грубую погрешность, если:

                                                                       (16)

где r = 3σ.

Иными словами, при выполнении условия (16), гипотезу о том, что данное отклонение получилось вследствие обычного рассеивания результатов измерений, отвергают.

При большом числе измерений (n≥30) в качестве σ можно принять ее оценку, задаваемую формулой (15). Если измеренное значение X_j содержит грубую погрешность, то это значение из рассмотрения исключают, вычисляют новое среднее значение:

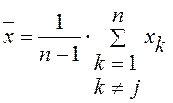
и проверяют следующее значение на предмет промаха. Эту процедуру повторяют до тех пор, пока не исключат все промахи.

При малом числе измерений и неизвестной дисперсии гипотезу об отсутствии промахов в j-ом измерении отвергают, если выполняется условие (15) при:

                                                                    (17)

где- коэффициент Стьюдента, определяемый из таблицы прил.2;

S² – выборочная дисперсия

Величина зависит от n и уровня значимости α. При α= 0,0027 и n>30,  t ≈3.

Таким образом, обработка результатов в общем случае сводится к исключению промахов /формулы (16) и (17)/, вычислению оценки истинного значения измеряемой величины /формула (II)/  и по заданному уровню значимости или доверительной вероятности доверительного интервала /формула (10) и (14)/.

При всех вычислениях необходимо помнить, что после каждого промаха число обрабатываемых измерений уменьшается на единицу, т.к. результаты измерений, содержащие промахи, исключаются из дальнейшего рассмотрения.