Машиностроение \ Метрология, стандартизация и сертификация

Качество и эффективность метрологического обеспечения, страница 15

- СКЗ равно  0,; 0,1; 0,2; 0,3. Распределение измеряемого параметра нормальное с нулевым средним и СКЗ равным σci, распределение погрешности измерения равномерное в интервале   ,  [11].

В таблице 1 представлены значения рисков заказчика (Rз) и поставщика (Rп), полученные в работе [5] методом имитационного моделирования для тридцати и пятнадцати контролируемых параметров.

Таблица 1.    Результаты расчета, приведённые в [5]

Vк(объём выборки), %

Риски

СКЗ σсi

СКЗ погрешности измерений σу

0

0.1

0.2

0.3

100

(k = 30)

Rз , %

0.8

0

0.09

0.14

0.17

0.9

0

0.37

0.60

0.76

1

0

0.98

1.66

2.11

Rп , %

0.8

0

0.15

0.41

0.85

0.9

0

0.56

1.36

2.60

1

0

1.26

2.98

5.38

50

(k = 15)

Rз , %

0.8

0.25*

0.3*

0.34*

0.35*

0.9

1.27*

1.49*

1.58*

1.67*

1

4.05*

4.54*

4.86*

5.15*

Rп , %

0.8

0

0.08

0.20

0.43

0.9

0

0.27

0.68

1.29

1

0

0.62

1.52

2.70

Таблица 2. Результаты расчёта по формулам (5) и (6)

 Число, контролируемых параметров

Риски

СКЗ σсi

СКЗ погрешности измерений σуi

0

0.1

0.2

0.3

k = 30

Rз = β, %

0.8

0

0.088

0.142

0.174

0.9

0

0.357

0.603

0.757

1

0

0.955

1.647

2.143

Rп = α, %

0.8

0

0.152

0.41

0.879

0.9

0

0.556

1.383

2.703

1

0

1.371

3.228

5.873

k = 15

Rз = β, %

0.8

0

0.044

0.071

0.087

0.9

0

0.179

0,302

0.379

1

0

0,479

0,827

1.077

Rп = α, %

0.8

0

0.076

0.205

0.44

0.9

0

0.278

0.694

1.361

1

0

0.688

1.627

2.981

В таблице 2 представлены расчёты ошибок первого и второго рода (α и β), т.е., рисков поставщика  Rп  и заказчика Rз соответственно, рассчитанные  по формулам (5) и (6). Сравнение данных таблиц 1 и 2 показывает достаточно хорошее совпадение результатов моделирования [5] и приведённых нами расчётов во всех случаях, кроме данных выделенных жирным шрифтом в обеих таблицах. В таблице 1 выделенные данные явно ошибочны, так как при нулевой погрешности измерений  риски заказчика должны быть так же нулевыми, Этот факт ещё раз подтверждает то, что результаты имитационного моделирования трудно проверить, даже самому автору [5] и, причём, для условий простейшего примера.

На рисунке 1 представлены графики зависимостей суммарных затрат (10) от погрешностей измерения ∆y  и числа контролируемых параметров n = 5, 15, 30 при тех же исходных данных, приведённых выше,  для условных значений коэффициентов затрат и  = 40.

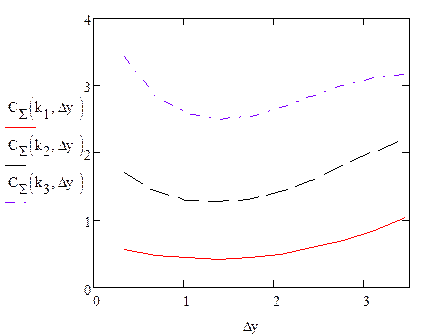
Рис. 1. Зависимость суммарных затрат (10) от погрешностей измерения при числе контролируемых параметров  k1 = 5, k2 = 15, k3 = 30.

Из рисунка 1 следует, что существуют минимумы суммарных затрат (10) при измерительном контроле  многопараметрического объекта в зависимости от погрешностей измерения. При этом, чем больше число контролируемых параметров и чем дороже потери на риски поставщика и заказчика, тем минимумы резче. Модель (10) позволяет рассчитать суммарные затраты на измерения при любом конечном числе контролируемых параметров изделия и для произвольных законов распределения вероятностей параметров и погрешностей измерения.

Скачать файл