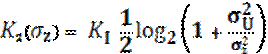Качество и эффективность метрологического обеспечения, страница 11

.                                                   (7)

Здесь – коэффициенты затрат в денежном эквиваленте;

 - СКЗ измеренного z и действительного U_c сигнала в формуле (5).

Формула (6) определена для модели  затрат (3), а выражение (7) определяется стоимостью количества информации, полученного при измерении параметра U (показателя качества) [6, 7,8, 9,10].

В формуле (4) вероятности ошибок первого и второго рода определяются с использованием ненормированных функций распределения показателя качества, которые разделены на три группы [5]:

Эти распределения определяются следующими выражениями:

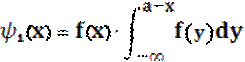,                                             (8)                                                     

,                                                   (9)                                              

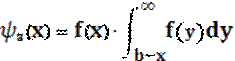.                                             (10)                                     

В (8),(9) и (10) f(x) и f(y) – плотности вероятностей измеряемого параметра x и аддитивной погрешности измерения y соответственно, [a,b]- допуск на измеряемый параметр.

Вероятности ошибок первого и второго рода определяются по следующим формулам[5]:

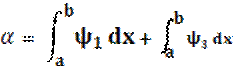,                                          (11)

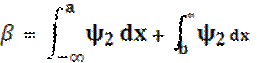                                      .                                          (12)

Далее рассмотрен пример для случая нормальных распределений параметра х и аддитивной погрешности измерения у  при нулевых мультипликационной  и систематической погрешностях. Плотности вероятности f(x) f(y) в обозначениях Mathcad имеют вид:

f(x) = dnorm(x, μ_x, σ_x),

f(y) = dnorm(y, μ_y, σ_y), где μ_x, μ_y – математические ожидания, σ_x, σ_y – среднеквадратические значения величин х и у соответственно.

Ошибка первого рода (риск поставщика):

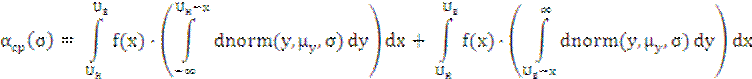, где σ = σ_y – СКЗ  погрешности измерения,  U_н, U_в – соответственно нижняя и верхняя границы поля допуска измеряемого параметра.

Зависимость α_ср (σ) представлена на рис. 1 при σ =  =1, 2…20.

График построен при следующих условных значениях:  μ_x = U_ном = 0, μ_у = 0; σ_x = 5; U_в = 5, U_н = -5.

Ошибка второго рода (риск заказчика):

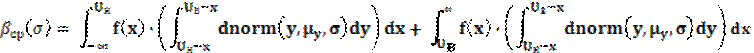
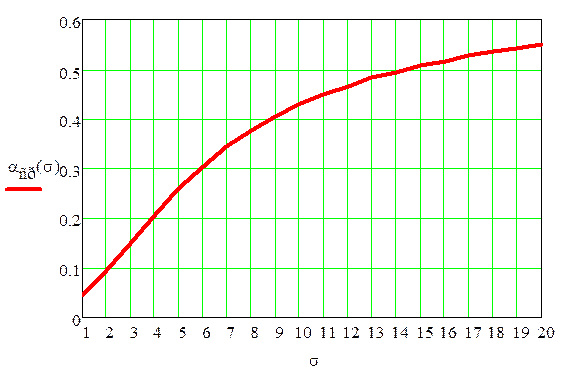
Рис.1. Зависимость ошибки первого рода от СКО погрешности измерения

Зависимость β_ср(σ) изображена на рис. 2 при тех же значениях, что и для графика на рисунке 1.При этом также:  σ = .

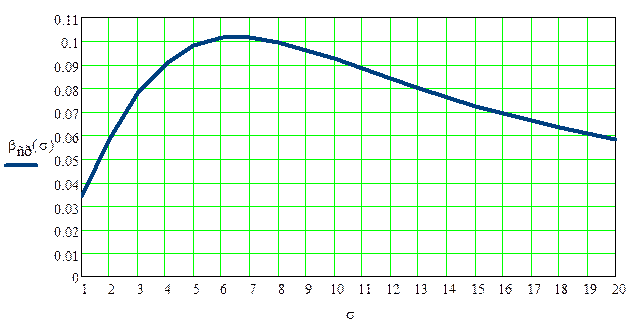
Рис. 2. Зависимость ошибки второго рода от СКО погрешности измерения

Суммарная функция затрат (4) при K_U = 1, K_α = 1 и K_β = 10 для  σ = .= 1, 2…10 представлена на рис. 3.

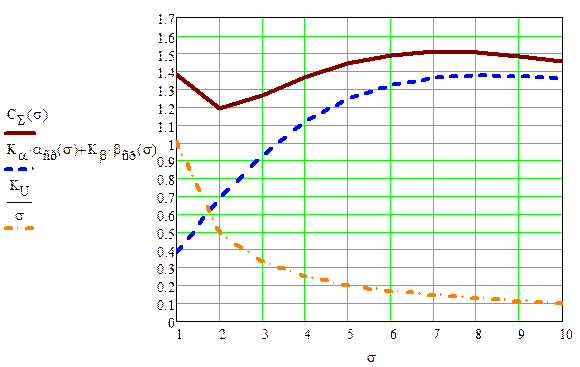
Рис. 3. С_Σ(σ) – суммарная функция затрат; K_α·α_ср(σ) + K_β·β_ср(σ) – затраты на потери из-за ошибок α и β; K_U/σ – затраты на измерение.

По графику на рис.3 можно определить оптимальное значение СКО погрешности измерения, при котором затраты минимальны. Наблюдаемое на рис. 3. уменьшение суммарных затрат определяется уменьшением ошибки второго рода (риска потребителя). Это происходит вследствие того, что при СКЗ погрешности измерения, много большем половины поля допуска, распределение вероятностей погрешности стремится к равномерному закону в интервале [0, ], и измерения не имеют смысла.

Для обобщённой модели (5) распределение вероятностей измеренного значения параметра (показателя качества) z  при нормальных распределениях мультипликативной ξ(t) и аддитивной Y(t) погрешностей будет также нормальным [7] с плотностью

f(z) = 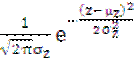 ,                                                         (13)                                                                                                            

где     μ_z= U_c+Δ_c;

σ_z=,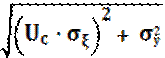

и  - СКЗ мультипликативной и аддитивной погрешностей.

Суммарные функции затрат  для моделей затрат на измерения (6) и (7) определяются выражениями:

,                                                          (14)

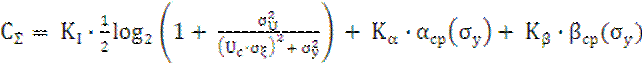.               (15)                                                                                                              

На рис. 4 представлены графики функций затрат (14) и (15) в зависимости от при значениях σ_ξ = 0.1,  = 1  с использованием формулы (13) для нормированных коэффициентов: K_U = 1, K_I = 1,   Kα = 1 и K_β = 10. Допуск на контролируемый параметр U_с находится в интервале [7.5, 12.5].