При наличии корреляции (Rti ≠ 0) между измеряемыми величинами
![]() , и оцениваемой величиной xi ошибка оценки уменьшается на
величину
, и оцениваемой величиной xi ошибка оценки уменьшается на
величину ![]() . Отсюда следует важный для
практики вывод, что при значениях суммы
. Отсюда следует важный для
практики вывод, что при значениях суммы 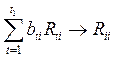 ошибка оценки
ошибка оценки ![]() стремится к нулю, т.е.
стремится к нулю, т.е.
![]() .
(9)
.
(9)
Это указывает на возможность
эффективного прогнозирования (оценки) неизмеряемого параметра xi,, контролируемого изделия по
измеряемым ![]() . При этом должны быть известны
характеристики M(xi), Rii, Rti, которые можно получить в
результате специально проведенного статистического анализа (на этапе обучения),
что вполне осуществимо в условиях серийного производства.
. При этом должны быть известны
характеристики M(xi), Rii, Rti, которые можно получить в
результате специально проведенного статистического анализа (на этапе обучения),
что вполне осуществимо в условиях серийного производства.
Поскольку условие (9) является
предельным, в действительности ошибка оценки ![]() , находится в интервале
, находится в интервале
![]() . (10)
. (10)
Следовательно, при использовании оценок (1) необходимо определить достоверность их применения для прогнозирования неизмеряемых параметров.
Условием годности изделия по параметру хi является принадлежность его заданному интервалу (допуску) [хiн ,xiв], т.е. условие
хiн ≤ xi ≤ xiв. (11) .
Замена xi его оценкой ![]() (1) в соответствии с
выражением (4) приводит к возникновению ошибок I и II рода при принятии
решения о годности изделия [1], аналогичных ошибкам измерения реальным прибором.
Для определения этих ошибок - рисков изготовителя α и заказчика β соответственно - применим
известный метод, использующий ненормированные функции распределения для частей
общей партии изделий, подлежащих контролю:
(1) в соответствии с
выражением (4) приводит к возникновению ошибок I и II рода при принятии
решения о годности изделия [1], аналогичных ошибкам измерения реальным прибором.
Для определения этих ошибок - рисков изготовителя α и заказчика β соответственно - применим
известный метод, использующий ненормированные функции распределения для частей
общей партии изделий, подлежащих контролю:
![]() (12)
(12)
- распределение вероятностей
оценки ![]() для части изделий, у которых истинное значение
параметра xi ≤ хiн;
для части изделий, у которых истинное значение
параметра xi ≤ хiн;
![]() (13)
(13)
-распределение вероятностей
оценки ![]() для изделий, у которых истинное значение xiнаходится в допуске, т.е. xiн < xi ≤ xiв;
для изделий, у которых истинное значение xiнаходится в допуске, т.е. xiн < xi ≤ xiв;
![]() (14)
(14)
- распределение вероятностей
оценки ![]() для изделий, у которых xi > xiв
для изделий, у которых xi > xiв
Здесь ![]() - плотность
вероятности оценки
- плотность
вероятности оценки ![]() , подчиняющаяся гауссовскому закону [2] с математическим
ожиданием M(xi) и дисперсией, определяемой по
формуле (6);
, подчиняющаяся гауссовскому закону [2] с математическим
ожиданием M(xi) и дисперсией, определяемой по
формуле (6); ![]() плотность вероятности случайной ошибки (нормальное
условное распределение) с математическим ожиданием [2]
плотность вероятности случайной ошибки (нормальное
условное распределение) с математическим ожиданием [2] ![]() и
дисперсией
и
дисперсией ![]() , определяемой по формуле (7).
, определяемой по формуле (7).
Условием нормировки для ![]() ,
, ![]() ,
, ![]() является
выражение [1]
является
выражение [1]
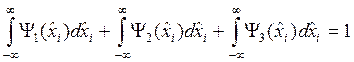
При известных распределениях (12)...(14) вероятность ошибки I и II рода определяется выражениями:
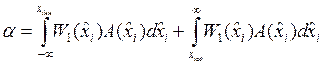 ,
(15)
,
(15)
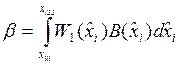 , (16)
, (16)
где
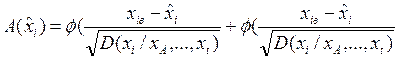 , (17)
, (17)
В работе [5] используется понятие контрольных допусков [хiн.к, xiв.к] на оцениваемые параметры, который в общем случае не совпадает с допуском по техническим условиям [хiн, xiв]. При этом границы контрольных допусков хiн.к, xiв.к находятся по требуемым значениям α и β. Методика выбора параметров для измерений и прогнозирования заключается в следующем.
Номенклатура параметров, часть которых измеряется, а
часть прогнозируется, определяется по следующим правилам. При попадании оценки
параметра ![]() в контрольное поле допуска [хiн.к, xiв.к] изделие по данному параметру считается годным, в
противном случае выполняется дополнительное измерение параметра xi .
в контрольное поле допуска [хiн.к, xiв.к] изделие по данному параметру считается годным, в
противном случае выполняется дополнительное измерение параметра xi .
Оптимальные контролируемые и прогнозируемые (оцениваемые) параметры выбираются по критерию уменьшения затрат при применении прогноза части параметров по сравнению с затратами спна полный контроль. При этом относительное уменьшение затрат равно
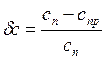 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.