Качество и эффективность метрологического обеспечения, страница 12

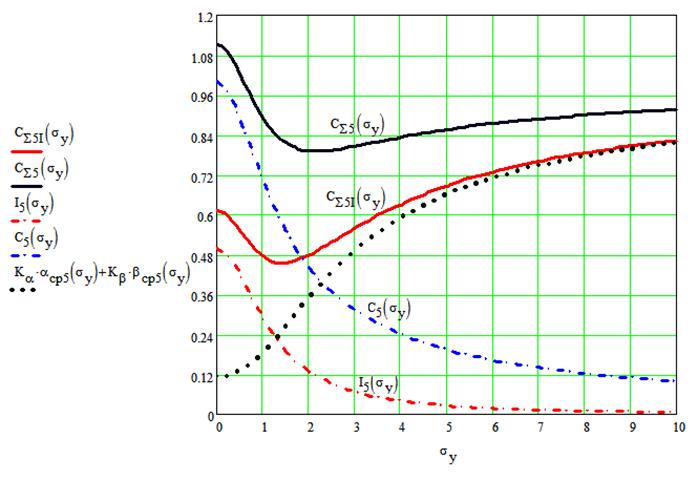
Рис. 4. Графики функций затрат.

Обозначения  графиков на рис.4:

- суммарные затраты по модели (14);

 - суммарные затраты по модели (15);

 - затраты на измерения по модели (7);

- затраты на измерения по модели (6):

 - суммарные потери из-за ошибок первого и второго рода.   

Из графиков, представленных на рис.4, следует:

1.Затраты на измерения  и  имеют убывающий характер. Различие этих зависимостей объясняется разностью применяемых моделей  (6) и (7). Эта разность заключается в том, что модель (6) является эмпирической в отличие от (7), и применяемые  коэффициенты затрат  K_U и K_I  имеют разную размерность

2.Затраты из-за потерь качества измерений

П =  одинаковы для обеих моделей (6) и (7) и имеют возрастающий характер от СКЗ погрешности  измерения, что соответствует принципу Г. Тагути.

3.Зависимости суммарных затрат, определяемые формулами  (14) и (15), имеют чётко выраженные минимумы, что позволяет определять оптимальные значения погрешностей измерения. Отличия этих зависимостей объясняются отличиями функций затрат на измерения   и   (см. п.1).

Выводы

1.  Предложены две модели (14) и (15) суммарных затрат, включающих затраты на проведение измерений по моделям (6), (7) и затраты за счёт потерь качества измерений для обобщённой измерительной модели (5), учитывающей мультипликативные, аддитивные и систематические погрешности измерения. Применение этих моделей при разработке метрологического обеспечения продукции (услуги) позволяет определять оптимальные или близкие к ним требования к значениям мультипликативных, аддитивных и систематических погрешностей при измерениях в нормальных и реальных [12] условиях.

2.  Применение модели (15) является более предпочтительным, так как функция затрат на измерения (7) и функция (15) в отличие от (3) и (6) не являются эмпирическими, а математически обоснованы и учитывают требования на измеряемый показатель качества, его статистические характеристики и статистические характеристики погрешностей измерения.

3.  Для практического применения функций суммарных затрат (14) и (15) необходимо определить реальные коэффициенты затрат для конкретного вида продукции  или услуги.

. В.И.Серых , С.П. Порватов, В.И. Сединин

МНОГОПАРАМЕТРИЧЕСКИЙ КОНТРОЛЬ ПРОДУКЦИИ

Введение

Наличие современного метрологического обеспечения производства продукции является необходимым условием при выполнении обязательных требований по мониторингу и измерению процессов и продукции [1]. При разработке метрологического обеспечения  продукции решаются следующие основные задачи [2,3]: определение рациональной номенклатуры контролируемых параметров, формирование требований к точности измерений, выбор средств измерений и выбор или  разработка методик выполнения измерений.

Задача рационального выбора номенклатуры контролируемых параметров с учётом статистических связей между ними рассматривалась в работах [13, 16] с использованием методов регрессионного анализа, где показана высокая эффективность применения этих методов.

В настоящей работе рассматривается метрологическая задача формирования требований к точности измерительного контроля многопараметрических объектов (продукции) при заданных требованиях на суммарные затраты, включающие затраты на проведение контрольных операций и на потери, определяемые качеством измерений. В рекомендациях [2] для решения указанной задачи предложена приближённая модель затрат, в которой предполагается, что затраты на измерения обратно пропорциональны погрешности измерений, а потери пропорциональны квадрату погрешности измерений (см. формулу (9)). Как указано в [2], эта модель может быть использована лишь для ориентировочных расчётов.  В ней не учитываются требования на измеряемые параметры и статистические свойства измеряемых параметров и погрешностей измерения, зависящих в общем случае от качества технологических процессов и средств измерений (СИ).